# 哈希表理论基础

哈希表是根据关键码的值而直接进行访问的数据结构

一般哈希表都是用来快速判断一个元素是否出现在集合里。

# 哈希函数

假如要查询一个名字是否在一所学校里。

用哈希函数把学生的姓名直接映射为哈希表上的索引，然后就可以通过查询索引下标快速知道这位学生是否在这所学校里了。

哈希函数通过 hashCode 把名字转化为数值，一般 hashcode 是通过特定编码方式，可以将其他数据转化为不同的数值，这样就把学生名字映射为哈希表上的索引数字了。

哈希函数

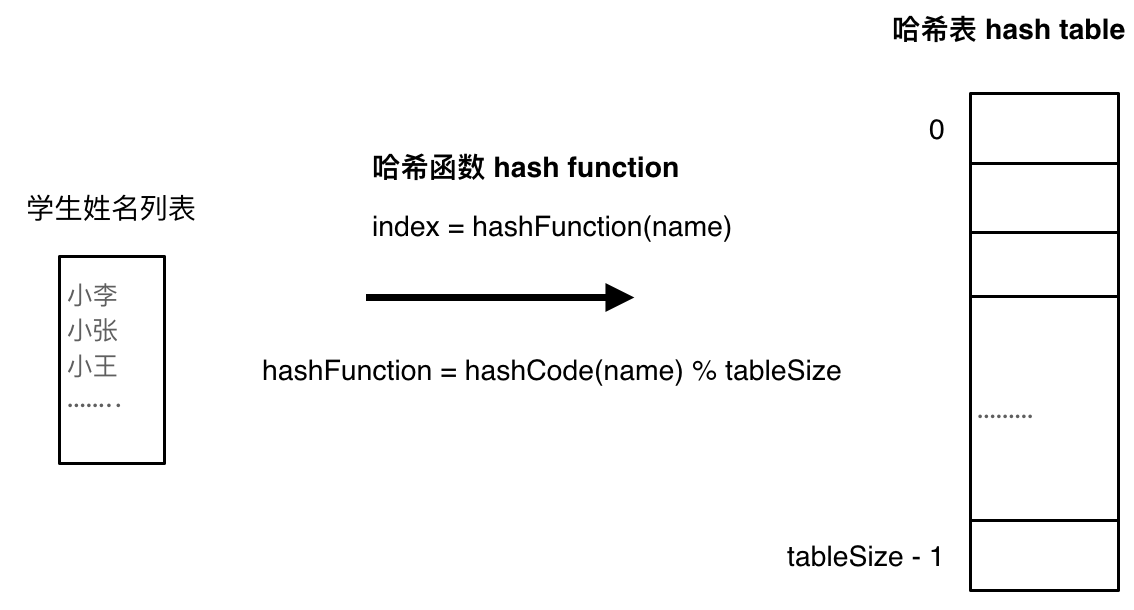
为了保证映射出来的索引都在哈希表上，会对数值再做一个取模的操作。

如果学生数量大于哈希表大小，难免会有几位学生的名字同时映射到哈希表同一索引下标的位置。

这就是哈希碰撞。

一般解决哈希碰撞有两种解决方式：拉链法和线性探测法。

将发生冲突的元素存储在链表当中。这样就可以通过索引找到元素。

拉链法要选择适当的哈希表大小，这样既不会因为数组空值而浪费大量的内存，也不会因为链表太长而在查找上浪费太多时间。

使用线性探测法，一定要保证 tableSize 大于 dataSize。我们需要依靠哈希表中的空位来解决碰撞问题。

例如冲突的位置，放了小李，那么就向下找一个空位放置小王的信息。所以要求 tableSize 一定要大于 dataSize ，要不然哈希表上就没有空置的位置来存放冲突的数据了。如图所示：

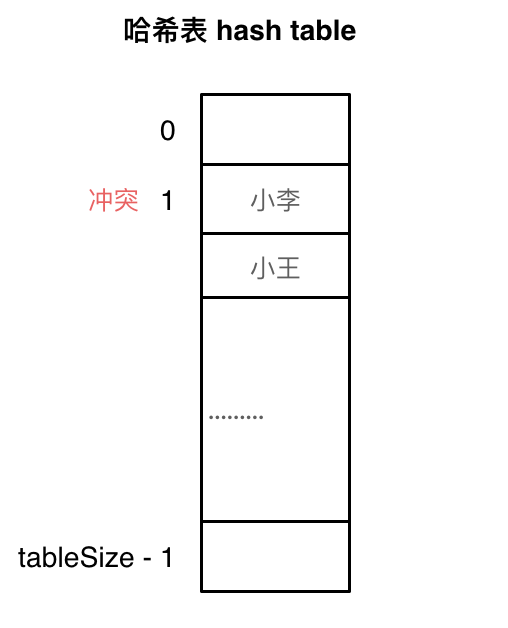
线性探测法

数组、set (集合)、map (映射)

C++ 中 set 和 map 各提供以下三种数据结构，底层实现以及优劣如下表所示：

集合	底层实现	是否有序	数值是否可以重复	能否更改数值	查询效率	增删改率
std::set	红黑树	有序	否	否	$O(log n )$	$O(log n)$
std::multiset	红黑树	有序	是	否	$O(log n)$	$O(log n)$
std::unordered_set	哈希表	无序	否	否	$O(1)$	$O(1)$

集合	底层实现	是否有序	数值是否可以重复	能否更改数值	查询效率	增删改率
std::map	红黑树	key 有序	key 不可重复	key 不可修改	$O(log n )$	$O(log n)$
std::multimap	红黑树	key 有序	key 可重复	key 不可修改	$O(log n)$	$O(log n)$
std::unordered_map	哈希表	key 无序	key 不可重复	key 不可修改	$O(1)$	$O(1)$