# 深度优先搜索理论基础

# DFS 和 BFS 的区别

• DFS 是向一个方向搜到底，搜不下去了才换方向回溯。
• BFS 是把本节点所连接的所有节点全遍历一遍，走到下一个节点的时候，再把连接节点的所有节点遍历一遍，搜索方向更像是广度，四面八方的搜索过程。

# DFS 的搜索过程

如图是一个无向图，我们要搜索从节点 1 到节点 6 的所有路径：

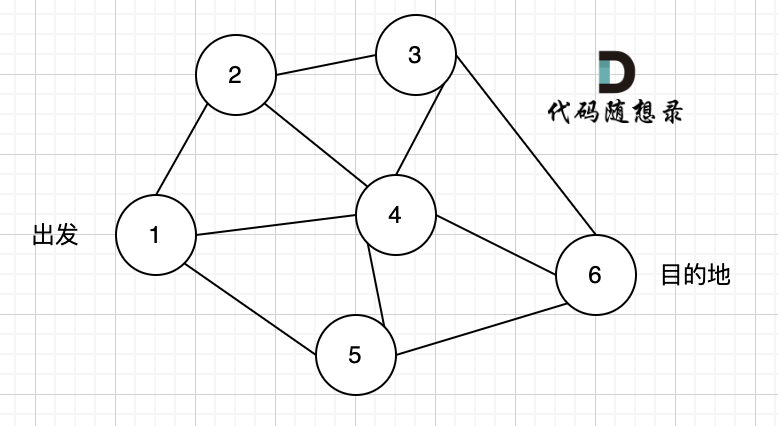
那么 dfs 搜索的第一条路径是这样的：

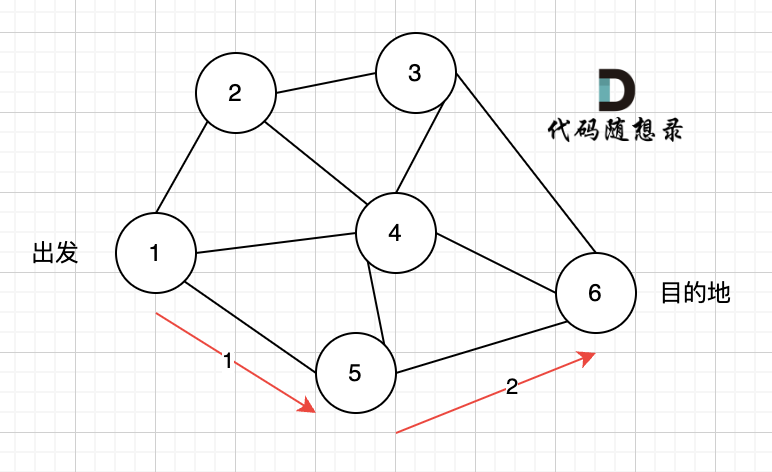
此时找到了 6，那么应该再去搜索其他方向了。

撤销了路径 2，然后改变方向走路径 3，接着也找到了 6. 撤销 2 改为路径 3 的过程就是回溯。

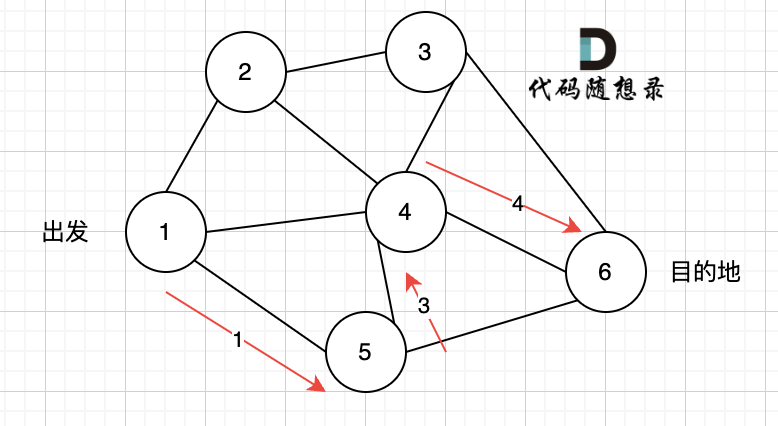
此时又到头了，撤销路径 4，改走路径 5：

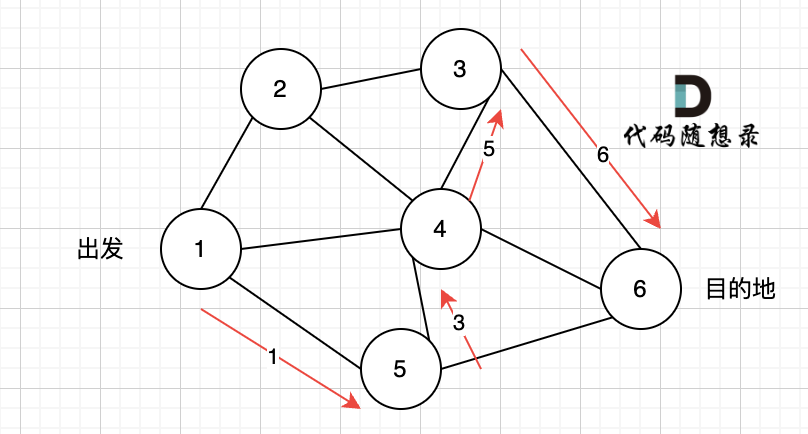
同理，撤销路径 6，改为路径 7、路径 8 和路径 7、路径 9，结果发现都走到了自己走过的节点。

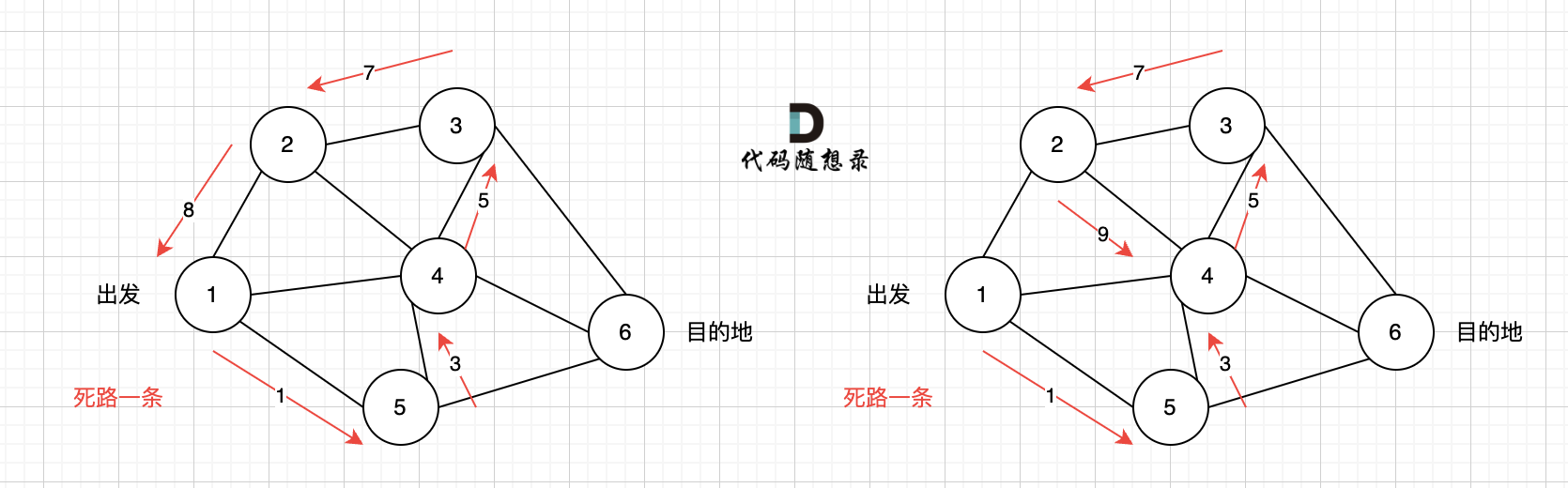
那么节点 2 所连接的路径和节点 3 所连接的都走过了，只能向上回退，撤销当初节点 4 的选择，也就是撤销路径 5，改为路径 10：

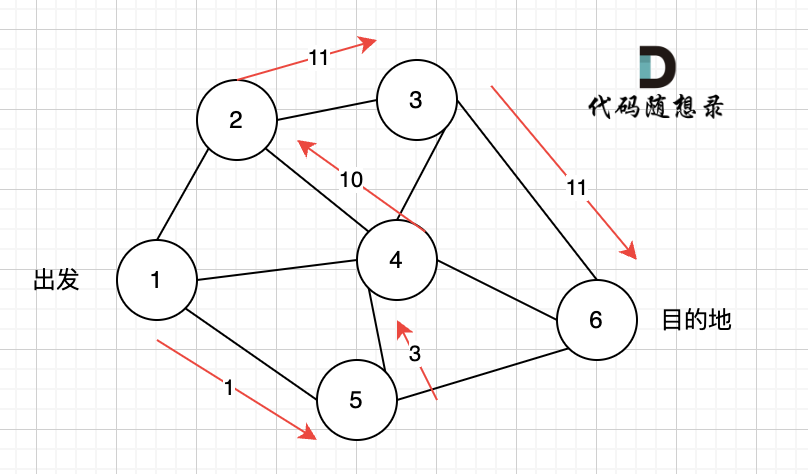
关键就两点：

• 搜索方向，是认准一个方向搜，直到碰壁之后再换方向
• 换方向是撤销原路径，改为节点链接的下一个路径，回溯的过程

# 代码框架

void dfs(参数) {

    if (终止条件) {

        存放结果;

        return;

    }

    for (选择：本节点所连接的其他节点) {

        处理节点;

        dfs(图，选择的节点); // 递归

        回溯，撤销处理结果

    }

}

1. 确定递归函数和参数

一般情况，深搜需要 二维数组数组结构保存所有路径，需要一维数组保存单一路径，这种保存结果的数组，我们可以定义一个全局变量，避免让我们的函数参数过多。

2. 确认终止条件

终止添加不仅是结束本层递归，同时也是我们收获结果的时候。

3. 处理目前搜索节点出发的路径

一般这里就是一个 for 循环的操作，去遍历 目前搜索节点 所能到的所有节点。