# 买卖股票的最佳时机 II

题目链接🔗

1. 确定 dp 数组以及下标的含义

• dp [i][0]: 表示第 i 天持有股票所得现金。
• dp [i][1]: 表示第 i 天不持有股票所得最多现金。

2. 确定递推公式

第 i 天持有股票即 dp [i][0]， 可以由两个状态推出来：

• 第 i-1 天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金 即：dp [i - 1][0]
• 第 i 天买入股票，所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即：dp [i - 1][1] - prices [i]

第 i 天不持有股票即 dp [i][1] 的情况， 依然可以由两个状态推出来：

• 第 i-1 天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金 即：dp [i - 1][1]
• 第 i 天卖出股票，所得现金就是按照今天股票价格卖出后所得现金即：prices [i] + dp [i - 1][0]

其他和买卖股票的最佳时机一致。

class Solution {

public:

    int maxProfit(vector<int>& prices) {

        int len = prices.size();

        vector<vector<int>> dp(len, vector<int>(2, 0));

        dp[0][0] -= prices[0];

        dp[0][1] = 0;

        for (int i = 1; i < len; i++) {

            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); // 注意这里是和 121. 买卖股票的最佳时机唯一不同的地方。

            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);

        }

        return dp[len - 1][1];

    }

};

# 买卖股票的最佳时机 III

题目链接🔗

和之前的买卖股票区别在于，将只能买卖一次限制改为了两次。

1. 确定 dp 数组以及下标的含义

有五个状态：

• 0：没有操作
• 1：第一次持有股票
• 2：第一次不持有股票
• 3：第二次持有股票
• 4：第二次不持有股票

dp [i][j]: 表示第 i 天状态 j 所剩最大现金。

2. 确定递推公式

dp [i][1] 状态，有两个具体操作：

• 操作一：第 i 天买入股票了，那么 dp [i][1] = dp [i-1][0] - prices [i]
• 操作二：第 i 天没有操作，而是沿用前一天买入的状态，即：dp [i][1] = dp [i - 1][1]

$$dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][1])$$

同理 dp [i][2] 也有两个操作：

• 操作一：第 i 天卖出股票了，那么 dp [i][2] = dp [i - 1][1] + prices [i]
• 操作二：第 i 天没有操作，沿用前一天卖出股票的状态，即：dp [i][2] = dp [i - 1][2]

$$dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])$$

同理剩下的状态为：

$$dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i])$$

$$dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i])$$

3. dp 数组如何初始化

第 0 天没有操作，这个最容易想到，就是 0，即：dp [0][0] = 0;

第 0 天做第一次买入的操作，dp [0][1] = -prices [0];

第 0 天第一次卖出可以理解为当天买入当天卖出，dp [0][2] = 0;

第 0 天第二次买入依赖于第一次卖出状态，相当于第 0 天买卖一次后又买了一次，dp [0][3] = -prices [0];

同理 dp [0][4] = 0。

4. 确定遍历顺序

从递归公式其实已经可以看出，一定是从前向后遍历，因为 dp [i]，依靠 dp [i - 1] 的数值。

5. 举例推导 dp 数组

以输入 [1,2,3,4,5] 为例：

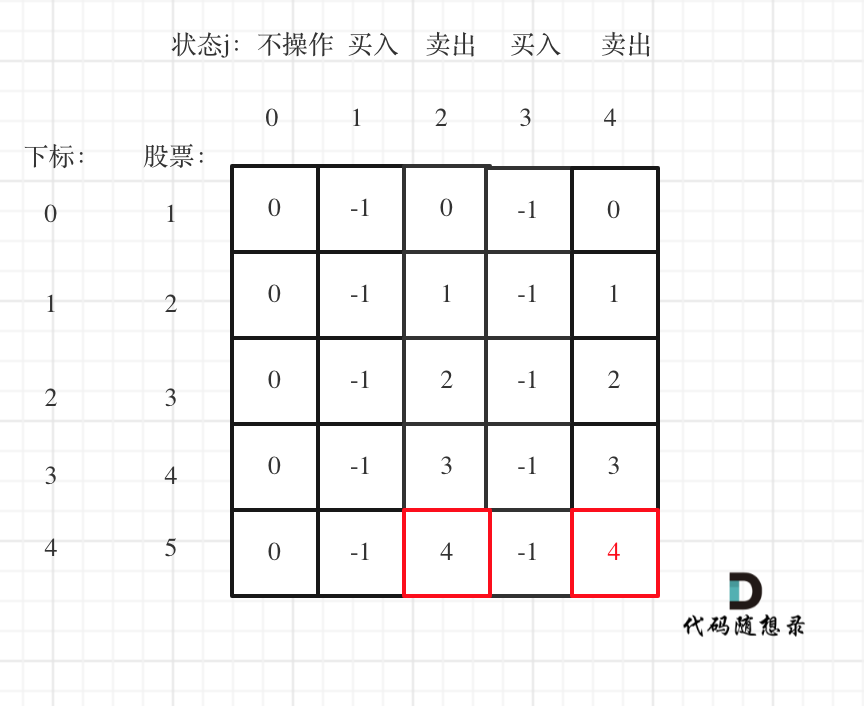
class Solution {

public:

    int maxProfit(vector<int>& prices) {

        if (prices.size() == 0) return 0;

        vector<vector<int>> dp(prices.size(), vector<int>(5, 0));

        dp[0][1] = -prices[0];

        dp[0][3] = -prices[0];

        for (int i = 1; i < prices.size(); i++) {

            dp[i][0] = dp[i - 1][0];

            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);

            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);

            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);

            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);

        }

        return dp[prices.size() - 1][4];

    }

};

# 买卖股票的最佳时机 IV

题目链接🔗

这题又把交易限制提升到了最多可以交易 k 次。

1. 确定 do 数组以及下标含义

根据之前买卖股票系列题，可以大概清楚。除了 0 以外，偶数就是卖出，奇数就是买入。

题目规定最多有 k 笔交易，那么数组开$2 \times k + 1$ 的空间。数组里面存两个状态：dp [i][1] 和 dp [i][2]。

2. 确定递推公式

达到 dp [i][1] 状态，有两个具体操作：

• 操作一：第 i 天买入股票了，那么 dp [i][1] = dp [i - 1][0] - prices [i]
• 操作二：第 i 天没有操作，而是沿用前一天买入的状态，即：dp [i][1] = dp [i - 1][1]

选最大的，所以 $$dp [i][1] = max (dp [i - 1][0] - prices [i], dp [i - 1][1])$$

同理 dp [i][2] 也有两个操作：

• 操作一：第 i 天卖出股票了，那么 dp [i][2] = dp [i - 1][1] + prices [i]
• 操作二：第 i 天没有操作，沿用前一天卖出股票的状态，即：dp [i][2] = dp [i - 1][2]

$$dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])$$

3. dp 数组如何初始化

根据前几道题的规律，dp [i][奇数] = -prices [0]，dp [i][偶数] = 0。

4. 确定遍历顺序

因为依靠 dp [i-1] 来决定状态，所以从前向后遍历

5. 举例推导 dp 数组

以输入 [1,2,3,4,5]，k=2 为例。

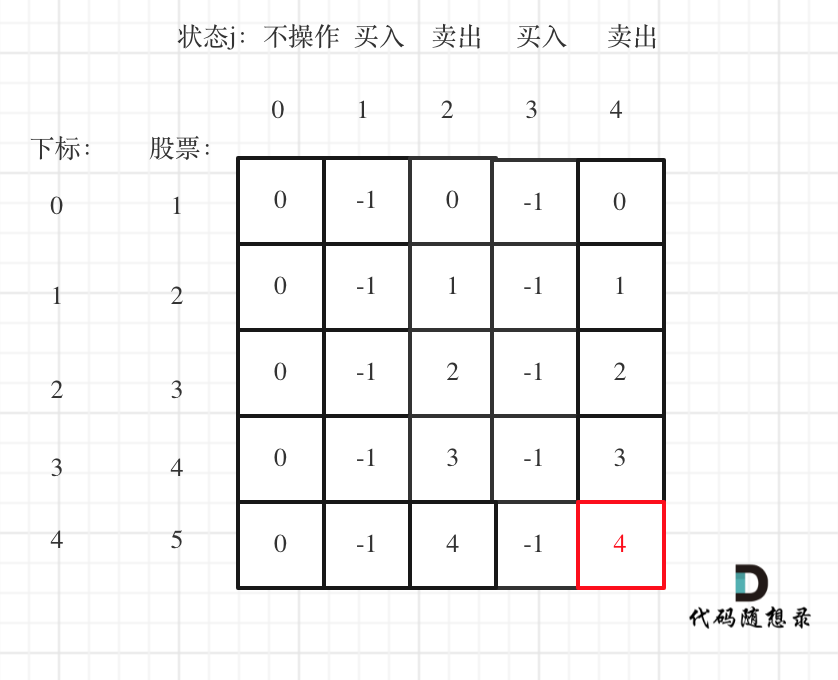
class Solution {

public:

    int maxProfit(int k, vector<int>& prices) {

        if (prices.size() == 0) return 0;

        vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));

        for (int j = 1; j < 2 * k; j += 2) {

            dp[0][j] = -prices[0];

        }

        for (int i = 1;i < prices.size(); i++) {

            for (int j = 0; j < 2 * k - 1; j += 2) {

                dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);

                dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);

            }

        }

        return dp[prices.size() - 1][2 * k];

    }

};

# 买卖股票的最佳时期含冷却期

题目链接🔗

这次又回到只能同时参与一次交易了，但是加上了卖出股票后，第二天不能买入的限制。

1. 确定 dp 数组以及下标的含义

dp [i][j]: 表示第 i 天状态为 j，所剩现金最多为 dp [i][j]。

j 具体可以分出四个状态

• 状态一：持有股票状态
• 状态二：保持卖出股票状态
• 状态三：今天卖出股票
• 状态四：今天为冷冻期状态，但不可持续，只有一天。

2. 确定递推公式

达到持有股票状态 dp [i][0] 有两个具体操作：

• 操作一：前一天就是持有股票状态（状态一），dp [i][0] = dp [i - 1][0]
• 操作二：今天买入了，有两种情况
  • 前一天是冷冻期（状态四），dp [i - 1][3] - prices [i]
  • 前一天是保持卖出股票的状态（状态二），dp [i - 1][1] - prices [i]

$$dp[i][0] = max(dp[i - 1][0], dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i])$$

达到保持卖出股票状态（状态二）即：dp [i][1]，有两个具体操作：

• 操作一：前一天就是状态二
• 操作二：前一天是冷冻期（状态四）
  dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);

达到今天就卖出股票状态（状态三），即：dp [i][2] ，只有一个操作，昨天一定是持有股票状态（状态一），今天卖出。

$$dp[i][2] = dp[i - 1][0] + prices[i]$$

达到冷冻期状态（状态四），即：dp [i][3]，只有一个操作，昨天卖出了股票（状态三）。

$$dp[i][3] = dp[i - 1][2]$$

3. dp 数组如何初始化

dp[0][0] = -prices[0]，dp[0][1] = dp[0][2] = dp[0][3] = 0。

4. 确定遍历顺序

从递归公式上可以看出，dp [i] 依赖于 dp [i-1]，所以是从前向后遍历。

5. 举例推导 dp 数组

以 [1,2,3,0,2] 为例:

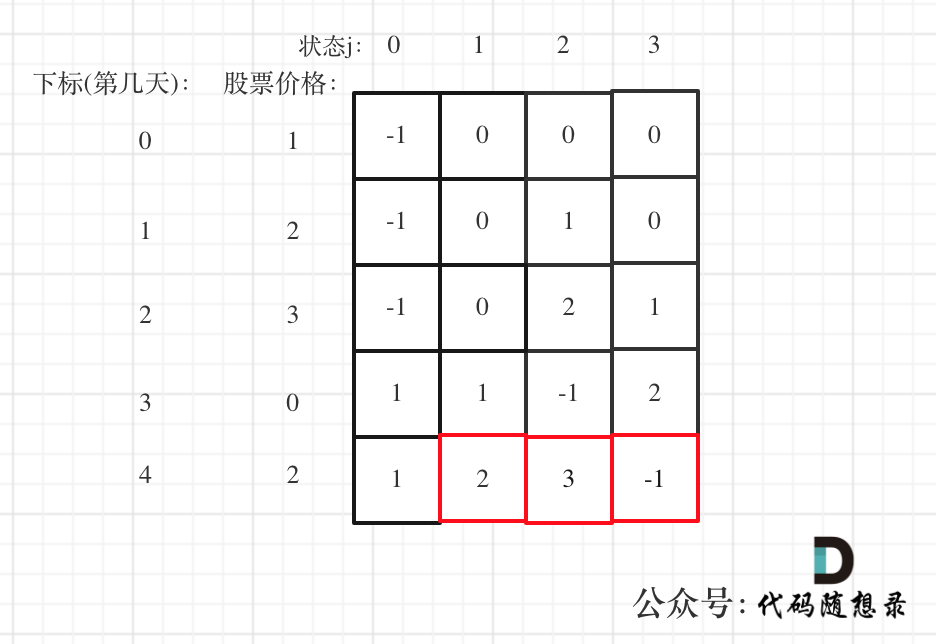
class Solution {

public:

    int maxProfit(vector<int>& prices) {

        int n = prices.size();

        if (n == 0) return 0;

        vector<vector<int>> dp(n, vector<int>(4, 0));

        dp[0][0] -= prices[0]; // 持股票

        for (int i = 1; i < n; i++) {

            dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]));

            dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);

            dp[i][2] = dp[i - 1][0] + prices[i];

            dp[i][3] = dp[i - 1][2];

        }

        return max(dp[n - 1][3], max(dp[n - 1][1], dp[n - 1][2]));

    }

};