# 打家劫舍
题目链接🔗
当前房屋偷不偷取决于前一个和前两个房间是否偷了。
当前状态和之前状态有依赖关系,使用动态规划。
- 确定 dp 数组以及下标的含义
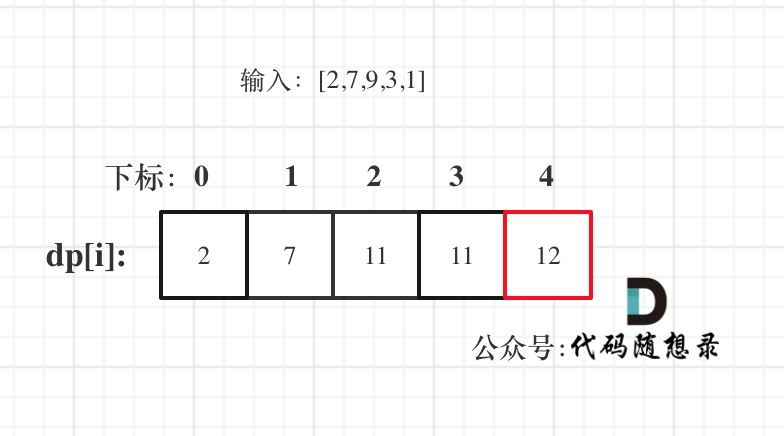
dp [i]: 考虑包括下标 i 以内的房屋,最多可以偷的金额为 dp [i]。
- 确定递推公式
决定 dp [i] 的因素就是第 i 房间偷还是不偷。
如果偷第 i 房间,那么 dp [i] = dp [i - 2] + nums [i] ,即:第 i-1 房一定是不考虑的,找出 下标 i-2(包括 i-2)以内的房屋,最多可以偷窃的金额为 dp [i-2] 加上第 i 房间偷到的钱。
如果不偷第 i 房间,那么 dp [i] = dp [i - 1],即考 虑 i-1 房,(注意这里是考虑,并不是一定要偷 i-1 房)
然后 dp [i] 取最大值,递推公式为:$$dp [i] = max (dp [i - 2] + nums [i], dp [i - 1])$$
- dp 数组如何初始化
dp [0] 和 dp [1] 是递推公式的基础。
从定义上讲,dp [0] = nums [0],dp [1] = max (nums [0], nums [1])。
- 确定遍历顺序
dp [i] 是由 dp [i-2] 和 dp [i-1] 推导出来的,所以从前向后遍历。
- 举例推导 dp 数组
class Solution { | |
public: | |
int rob(vector<int>& nums) { | |
if (nums.size() == 0) return 0; | |
if (nums.size() == 1) return nums[0]; | |
vector<int> dp(nums.size()); | |
dp[0] = nums[0]; | |
dp[1] = max(nums[0], nums[1]); | |
for (int i = 2; i < nums.size(); i++) { | |
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]); | |
} | |
return dp[nums.size() - 1]; | |
} | |
}; |
# 打家劫舍 II
题目链接🔗
和上题的区别在于房屋成环了。
对于一个数组,成环的话要有以下三种情况考虑:
- 情况一:考虑不包含首尾元素
- 情况二:考虑包含首元素不包含尾元素
- 情况三:考虑包含尾元素,不包含首元素。
而情况二和情况三都包含了情况一了,所以只考虑情况二和情况三就可以了。
class Solution { | |
public: | |
int rob(vector<int>& nums) { | |
if (nums.size() == 0) return 0; | |
if (nums.size() == 1) return nums[0]; | |
int result1 = robRange(nums, 0, nums.size() - 2); // 情况二 | |
int result2 = robRange(nums, 1, nums.size() - 1); // 情况三 | |
return max(result1, result2); | |
} | |
// 198. 打家劫舍的逻辑 | |
int robRange(vector<int>& nums, int start, int end) { | |
if (end == start) return nums[start]; | |
vector<int> dp(nums.size()); | |
dp[start] = nums[start]; | |
dp[start + 1] = max(nums[start], nums[start + 1]); | |
for (int i = start + 2; i <= end; i++) { | |
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]); | |
} | |
return dp[end]; | |
} | |
}; |
# 打家劫舍 III
题目链接🔗
结构从数组又变成了二叉树。
# 暴力
用过用深搜的话,要用后序遍历,因为要用到返回值。
class Solution { | |
public: | |
unordered_map<TreeNode* , int> umap; // 记录计算过的结果 | |
int rob(TreeNode* root) { | |
if (root == nullptr) return 0; | |
if (root->left == nullptr && root->right == nullptr) return root->val; | |
if (umap[root]) return umap[root]; // 如果 umap 里已经有记录则直接返回 | |
// 偷父节点 | |
int val1 = root->val; | |
if (root->left) val1 += rob(root->left->left) + rob(root->left->right); // 跳过 root->left | |
if (root->right) val1 += rob(root->right->left) + rob(root->right->right); // 跳过 root->right | |
// 不偷父节点 | |
int val2 = rob(root->left) + rob(root->right); // 考虑 root 的左右孩子 | |
umap[root] = max(val1, val2); //umap 记录一下结果 | |
return max(val1, val2); | |
} | |
}; |
# 树形 dp
使用一个长度为 2 的数组,记录当前节点偷与不偷所得到的的最大金钱。
- 确定递归函数参数和返回值
这里我们要求一个节点 偷与不偷的两个状态所得到的金钱,那么返回值就是一个长度为 2 的数组。
这个返回的数组就是 dp 数组。
dp 数组下标为 0 记录不偷该节点所得到的的最大金钱,下标为 1 记录偷该节点所得到的的最大金钱。
- 确定终止条件
如果遇到空节点的话,很明显,无论偷还是不偷都是 0,所以就返回。
这也相当于 dp 数组初始化。
- 确定遍历顺序
首先明确的是使用后序遍历。 因为要通过递归函数的返回值来做下一步计算。
通过递归左节点,得到左节点偷与不偷的金钱。
通过递归右节点,得到右节点偷与不偷的金钱。
- 确定单层递归逻辑
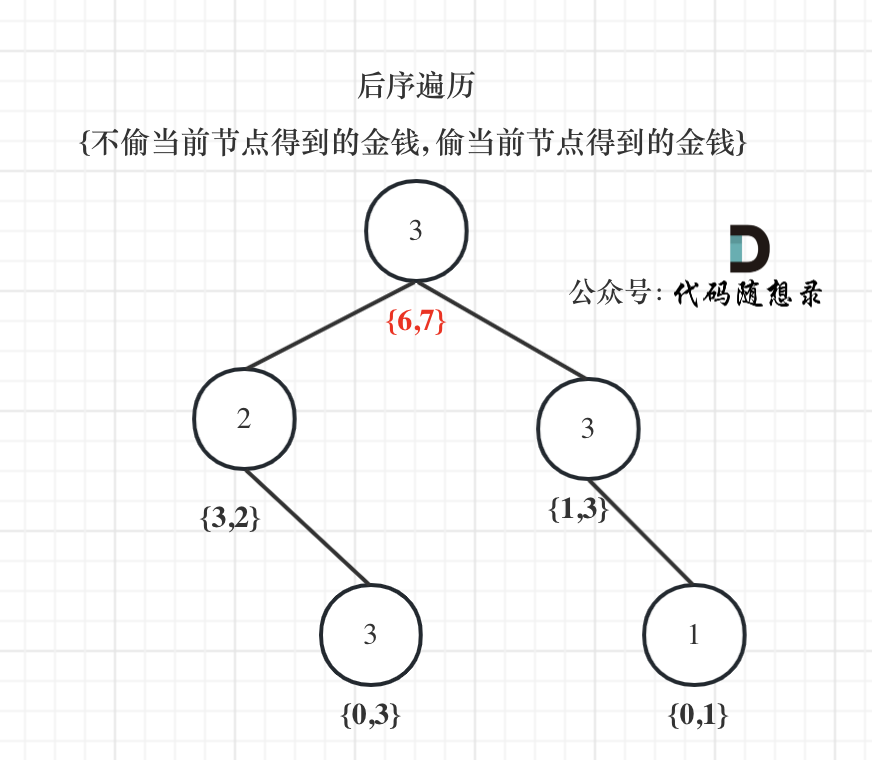
如果是偷当前节点,那么左右孩子就不能偷 $$val1 = cur->val + left [0] + right [0]$$
如果不偷当前节点,那么左右孩子就可以偷,至于到底偷不偷一定是选一个最大的,所以 $$val2 = max (left [0], left [1]) + max (right [0], right [1])$$
最后当前节点的状态就是
- 举例推导 dp 数组
class Solution { | |
public: | |
int rob(TreeNode* root) { | |
vector<int> result = robTree(root); | |
return max(result[0], result[1]); | |
} | |
// 长度为 2 的数组,0:不偷,1:偷 | |
vector<int> robTree(TreeNode* cur) { | |
if (cur == NULL) return vector<int>{0, 0}; | |
vector<int> left = robTree(cur->left); | |
vector<int> right = robTree(cur->right); | |
// 偷 cur,那么就不能偷左右节点。 | |
int val1 = cur->val + left[0] + right[0]; | |
// 不偷 cur,那么可以偷也可以不偷左右节点,则取较大的情况 | |
int val2 = max(left[0], left[1]) + max(right[0], right[1]); | |
return {val2, val1}; | |
} | |
}; |
# 买卖股票的最佳时机
题目链接🔗
# 贪心
因为股票就买卖一次,那么贪心的想法很自然就是取最左最小值,取最右最大值,那么得到的差值就是最大利润。
class Solution { | |
public: | |
int maxProfit(vector<int>& prices) { | |
int low = INT_MAX; | |
int result = 0; | |
for (int i = 0; i < prices.size(); i++) { | |
low = min(low, prices[i]); // 取最左最小价格 | |
result = max(result, prices[i] - low); // 直接取最大区间利润 | |
} | |
return result; | |
} | |
}; |
# 动态规划
- 确定 dp 数组以及下标的含义
- dp [i][0]: 表示第 i 天持有股票所得最多现金。
- dp [i][1]: 表示第 i 天不持有股票所得最多现金。
一开始现金是 0,那么加入第 i 天买入股票现金就是 - prices [i],这是一个负数。
- 确定递推公式
第 i 天持有股票即 dp [i][0] 可以由两个状态推出来:
- 第 i-1 天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp [i - 1][0]
- 第 i 天买入股票,所得现金就是买入今天的股票后所得现金即:-prices [i]
dp [i][0] 应该选所得现金最大的,所以 $$dp [i][0] = max (dp [i - 1][0], -prices [i])$$
第 i 天不持有股票即 dp [i][1] 可以由两个状态推出来:
- 第 i-1 天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp [i - 1][1]
- 第 i 天卖出股票,所得现金就是按照今天股票价格卖出后所得现金即:prices [i] + dp [i - 1][0]
同样 dp [i][1] 取最大的 $$dp [i][1] = max (dp [i - 1][1], prices [i] + dp [i - 1][0])$$
- dp 数组如何初始化
基础都是要从 dp [0][0] 和 dp [0][1] 推导出来。
dp [0][0] 表示第 0 天持有股票,此时的持有股票就一定是买入股票了,所以 dp [0][0] -= prices [0]
dp [0][1] 表示第 0 天不持有股票,不持有股票那么现金就是 0,所以 dp [0][1] = 0
- 确定遍历顺序
从递推公式可以看出 dp [i] 都是由 dp [i - 1] 推导出来的,那么一定是从前向后遍历。
- 举例推导 dp 数组
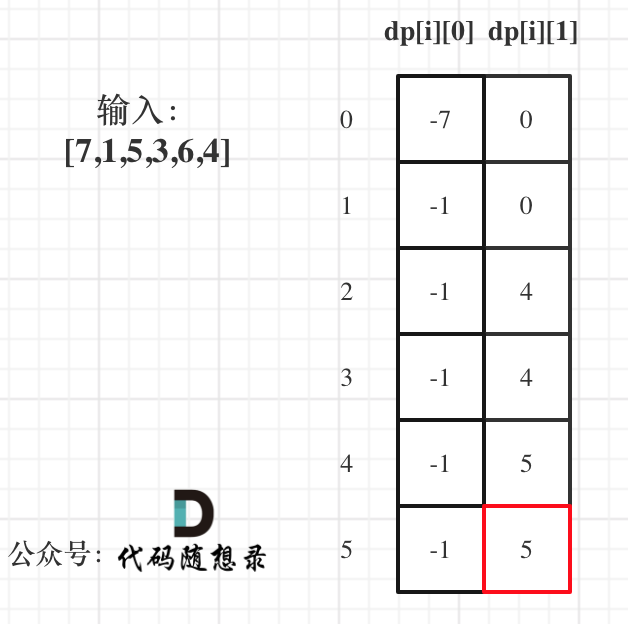
因为不持有股票的状态一定比持有状态的余额多,所以取 dp [5][1]。
class Solution { | |
public: | |
int maxProfit(vector<int>& prices) { | |
int len = prices.size(); | |
if (len == 0) return 0; | |
vector<vector<int>> dp(len, vector<int>(2)); | |
dp[0][0] -= prices[0]; | |
dp[0][1] = 0; | |
for (int i = 1; i < len; i++) { | |
dp[i][0] = max(dp[i - 1][0], -prices[i]); | |
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]); | |
} | |
return dp[len - 1][1]; | |
} | |
}; |