# 不同路径
题目链接🔗
机器人要从 (0, 0) 走到 (m-1, n-1)。
- 确定 dp 数组以及下标的含义
dp [i][j]: 从 (0, 0) 到 (i, j) 有 dp [i][j] 条不同的路径。
- 确定递推公式
dp 可以从两个方向推导出来,即 dp [i-1][j] 和 dp [i][j-1]。
那么
- dp 数组初始化
dp [i][0] 和 dp [0][j] 都为 0,因为从 (0,0) 到 (i,0) 或者 (0,j) 的路径只有一条
- 确定遍历顺序
dp [i][j] 是从上方和左方推导出来,那么从左到右一层一层遍历即可。
- 举例推导 dp 数组
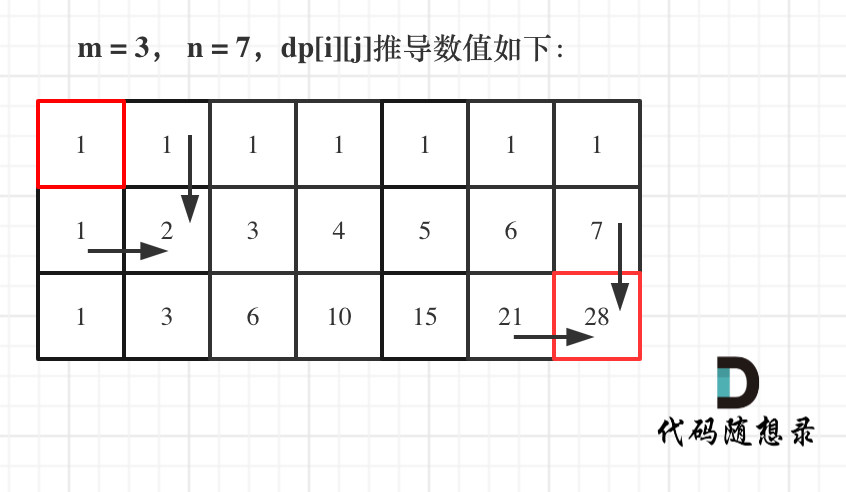
class Solution { | |
public: | |
int uniquePaths(int m, int n) { | |
vector<vector<int>> dp(m, vector<int>(n, 0)); | |
for (int i = 0; i < m; i++) dp[i][0] = 1; | |
for (int j = 0; j < n; j++) dp[0][j] = 1; | |
for (int i = 1; i < m; i++) { | |
for (int j = 1; j < n; j++) { | |
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; | |
} | |
} | |
return dp[m - 1][n - 1]; | |
} | |
}; |
# 不同路径 II
题目链接🔗
和上题描述区别在于有障碍了,但动态规划思路不变。
在没有碰到障碍的时候,dp 数组正常的递推,碰到障碍就跳过。
class Solution { | |
public: | |
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) { | |
int m = obstacleGrid.size(); | |
int n = obstacleGrid[0].size(); | |
if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) // 如果在起点或终点出现了障碍,直接返回 0 | |
return 0; | |
vector<vector<int>> dp(m, vector<int>(n, 0)); | |
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1; | |
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1; | |
for (int i = 1; i < m; i++) { | |
for (int j = 1; j < n; j++) { | |
if (obstacleGrid[i][j] == 1) continue; | |
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; | |
} | |
} | |
return dp[m - 1][n - 1]; | |
} | |
}; |
# 整数拆分
题目链接🔗
- 确定 dp 数组以及下标的含义
dp [i]: 拆分数字 i,可以得到最大的乘积 dp [i]。
- 确定递推公式
最大乘积是怎么来的。
j 是从 1 开始遍历到 i 的所有情况。
i 如果拆成两个数就是 ,如果拆成三个及以上就是 。
j 是从 1 开始遍历的,因此在 j 的拆分在遍历中都包含了。
递推公式就为
- dp 的初始化
从 dp 数组的定义讲,dp [0] 和 dp [1] 没有意义不需要初始化。
从 dp [2] 开始,dp [2] = 1。
- 遍历顺序
dp [i] 是依靠 dp [i - j] 的状态,所以遍历 i 一定是从前向后遍历,先有 dp [i - j] 再有 dp [i]。
i 从 3 开始遍历到 n,j 从 1 开始遍历遍历到。因为拆分一个数 n 使之乘积最大,那么一定是拆分成 m 个近似相同的子数相乘才是最大的。
- 举例推导 dp 数组
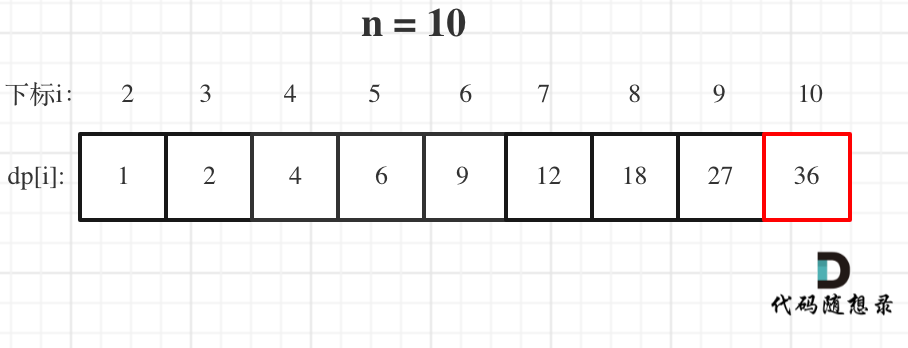
class Solution { | |
public: | |
int integerBreak(int n) { | |
vector<int> dp(n + 1); | |
dp[2] = 1; | |
for (int i = 3; i <= n ; i++) { | |
for (int j = 1; j <= i / 2; j++) { | |
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j)); | |
} | |
} | |
return dp[n]; | |
} | |
}; |
# 不同的二叉搜索树
题目链接🔗
n 为 1 和 n 为 2 很简单,从 n 为 3 开始:
父节点为 1,右子树有两个节点,和 n 为 2 时的节点布局一样。
父节点为 2,左右子树各有一个节点,和 n 为 1 时的节点布局一样。
父节点为 3,左子树有两个节点,和 n 为 2 时的节点布局一样。
dp [3],就是 元素 1 为头结点搜索树的数量 + 元素 2 为头结点搜索树的数量 + 元素 3 为头结点搜索树的数量
元素 1 为头结点搜索树的数量 = 右子树有 2 个元素的搜索树数量 * 左子树有 0 个元素的搜索树数量
元素 2 为头结点搜索树的数量 = 右子树有 1 个元素的搜索树数量 * 左子树有 1 个元素的搜索树数量
元素 3 为头结点搜索树的数量 = 右子树有 0 个元素的搜索树数量 * 左子树有 2 个元素的搜索树数量
有 2 个元素的搜索树数量就是 dp [2]。
有 1 个元素的搜索树数量就是 dp [1]。
有 0 个元素的搜索树数量就是 dp [0]。
所以 dp [3] = dp [2] * dp [0] + dp [1] * dp [1] + dp [0] * dp [2]
- 确定 dp 数组以及下标含义
dp [i]: 1 到 i 为节点组成的二叉搜索树个数为 dp [i]。
或者 i 个不同元素节点组成的二叉搜索树的个数。
- 确定递推公式
用 j 相当于头结点元素,从 1 开始遍历到 i。
dp [i] += dp [以 j 为头结点左子树节点数量] * dp [以 j 为头结点右子树节点数量]
因为是二叉搜索树,所以 j 的左子树节点数为 j-1,右子树节点为 i-j。
递推公式:
- dp 的初始化
初始化 dp [0] = 1,推导的基础都是 dp [0]。
- 确定遍历顺序
节点数为 i 的状态是依靠 i 之前节点数的状态。
那么遍历 i 里面每一个数作为头结点的状态,用 j 来遍历。
- 举例推导 dp 数组
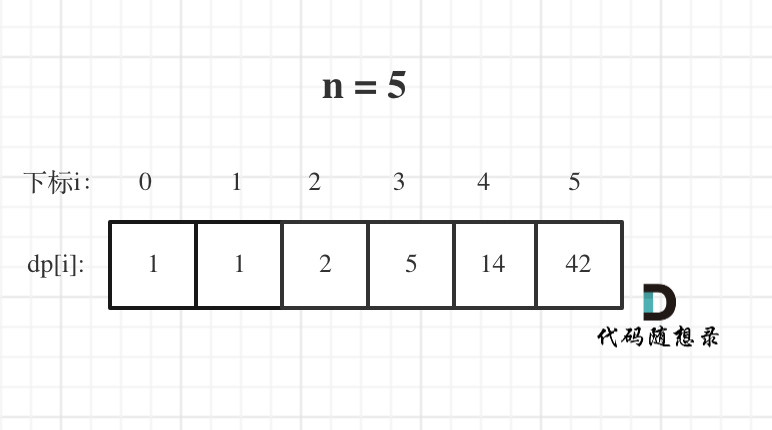
class Solution { | |
public: | |
int numTrees(int n) { | |
vector<int> dp(n + 1); | |
dp[0] = 1; | |
for (int i = 1; i <= n; i++) { | |
for (int j = 1; j <= i; j++) { | |
dp[i] += dp[j - 1] * dp[i - j]; | |
} | |
} | |
return dp[n]; | |
} | |
}; |