# 动态规划理论基础

动态规划中每一个状态一定是由上一个状态推导出来的。

对于动态规划问题，大致分为五步：

1. 确定 dp 数组以及下标的含义
2. 确定递推公式
3. dp 数组如何初始化
4. 确定遍历顺序
5. 举例推导 dp 数组

# 爬楼梯

题目链接🔗

1. 确定 dp 数组以及下标的含义

dp [i]: 爬到第 i 层有 dp [i] 种方法。

2. 确定递推公式

当前楼层可以由上一楼层或上上一楼层到达，因此 dp [i] 可以由两个方向推导出来。

首先是 dp [i-1]，上 i-1 层，有 dp [i-1] 种方法，那么再走一次爬一个楼层就是 dp [i]。

其次是 dp [i-2]，上 i-2 层，有 do [i-2] 种方法，那么再走一次爬两个楼层就是 dp [i]。

因此递推公式为：$dp[i] = dp[i-1] + dp[i-2]$。

3. dp 数组如何初始化

由题意可以推导出 dp [1] = 1，dp [2] = 2。

4. 确定遍历顺序

由递推公式可以看出遍历顺序是从前向后的。

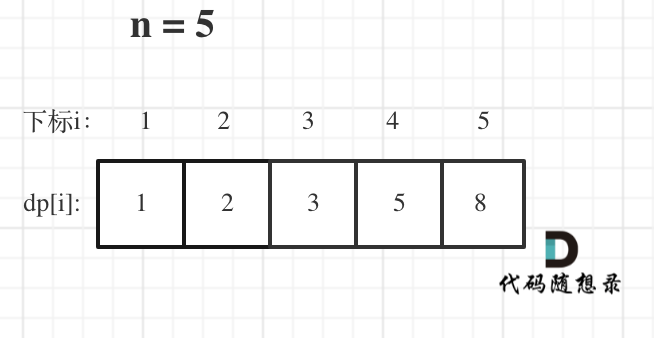
5. 举例推导 dp 数组

当 n=5 时，dp 数组如下：

class Solution {

public:

    int climbStairs(int n) {

        if (n <= 1) return n; // 因为下面直接对 dp [2] 操作了，防止空指针

        vector<int> dp(n + 1);

        dp[1] = 1;

        dp[2] = 2;

        for (int i = 3; i <= n; i++) { // 注意 i 是从 3 开始的

            dp[i] = dp[i - 1] + dp[i - 2];

        }

        return dp[n];

    }

};

# 使用最小花费爬楼梯

题目链接🔗

1. 确定 dp 数组以及下标的含义

dp [i]: 到达第 i 台阶所花费的最少体力

2. 确定递推公式

dp [i] 可以从两个途径得到，dp [i-1] 和 dp [i-2]。

dp [i-1] 跳到 dp [i] 的花费为 d [i-1] + cost [i-1]。

同理 dp [i-2] 跳到 dp [i] 的花费为 dp [i-2] + cost [i-2]。

两者选最小，递推公式为: $dp[i] = min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-2])$。

3. dp 数组如何初始化

可以选择从下表 0 或 1 的两个位置开始爬楼梯，向上爬需要花费体力，换言之在 0 和 1 两个位置是不花体力的。

dp[0] = dp[1] = 0。

4. 确定遍历顺序

从前向后遍历 cost 数组。

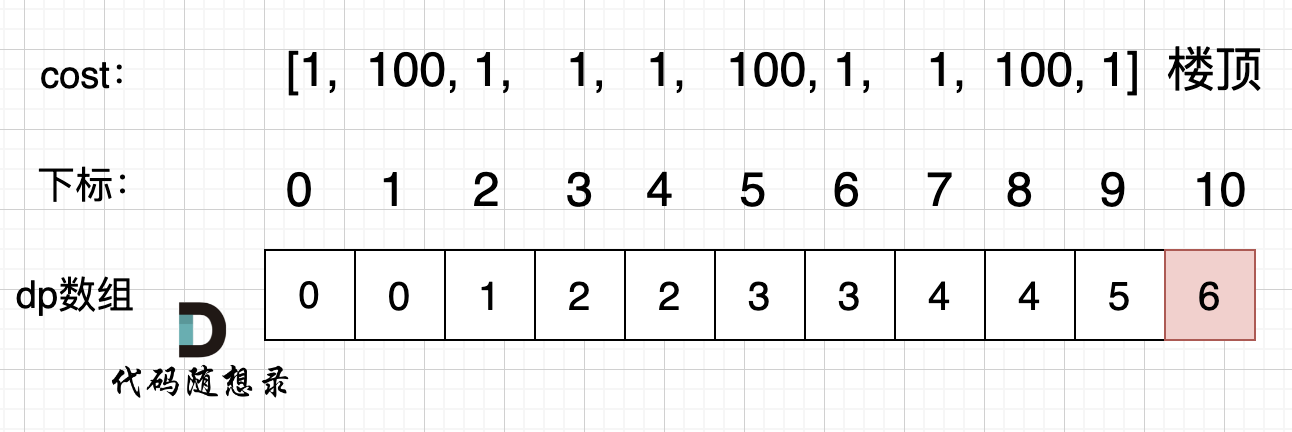
5. 举例推导 dp 数组

cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ，来模拟一下 dp 数组的状态变化：

class Solution {

public:

    int minCostClimbingStairs(vector<int>& cost) {

        vector<int> dp(cost.size() + 1);

        dp[0] = 0; // 默认第一步都是不花费体力的

        dp[1] = 0;

        for (int i = 2; i <= cost.size(); i++) {

            dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);

        }

        return dp[cost.size()];

    }

};