# 全排列
题目链接🔗
以 [1, 2, 3] 为例,将问题抽象成如下树形结构:
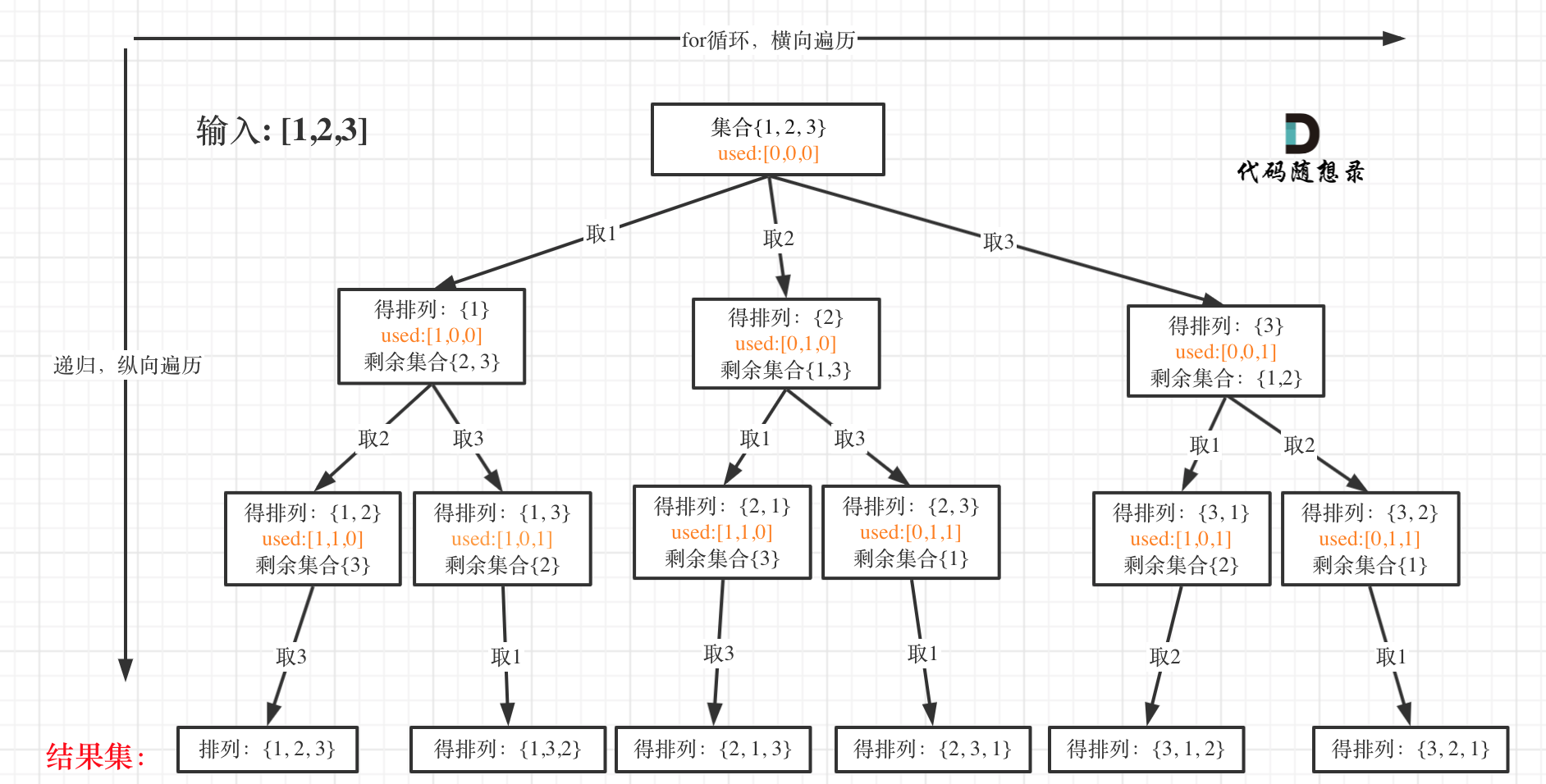
- 回溯函数参数和返回值
排列是有序的,所以 [1, 2] 和 [2, 1] 是两个集合,不需要像组合问题一样用 startIndex 控制起始位置。
但排列问题需要一个 used [] 数组来标记已选择元素。
- 终止条件
当到达叶子节点时终止,即 path.size() == nums.size() 。
- 单层搜索逻辑
用 used [] 数组来记录此时 path 里都有哪些元素使用了,一个排列里一个元素只能用一次。
class Solution { | |
public: | |
vector<vector<int>> result; | |
vector<int> path; | |
void backtracking (vector<int>& nums, vector<bool>& used) { | |
// 此时说明找到了一组 | |
if (path.size() == nums.size()) { | |
result.push_back(path); | |
return; | |
} | |
for (int i = 0; i < nums.size(); i++) { | |
if (used[i] == true) continue; //path 里已经收录的元素,直接跳过 | |
used[i] = true; | |
path.push_back(nums[i]); | |
backtracking(nums, used); | |
path.pop_back(); | |
used[i] = false; | |
} | |
} | |
vector<vector<int>> permute(vector<int>& nums) { | |
result.clear(); | |
path.clear(); | |
vector<bool> used(nums.size(), false); | |
backtracking(nums, used); | |
return result; | |
} | |
}; |
# 全排列 II
题目链接🔗
给定一个可包含重复数字的序列,要返回所有不重复的全排列。涉及去重。
去重前先对元素排序,然后对同一树层进行去重。
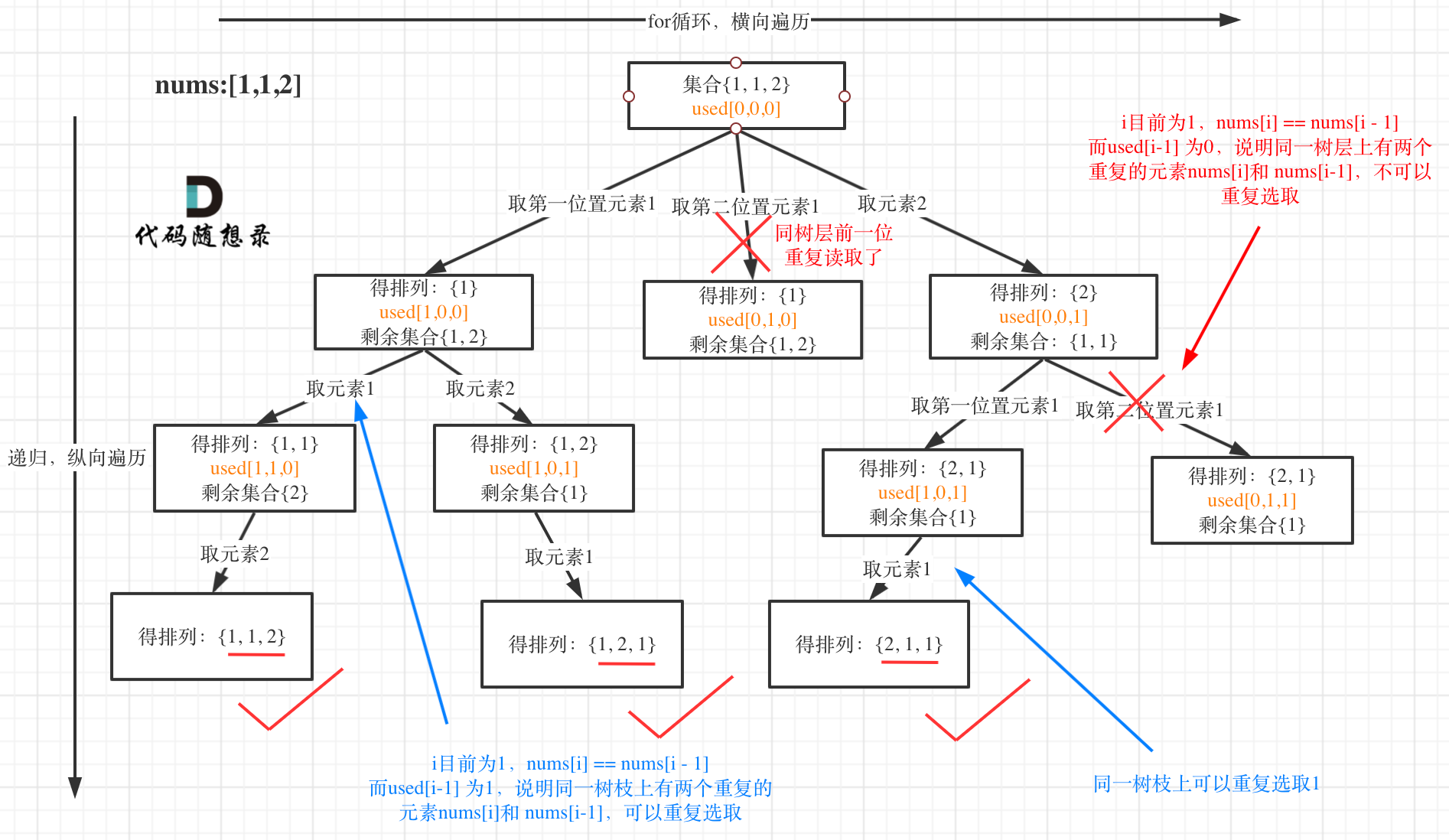
class Solution { | |
private: | |
vector<vector<int>> result; | |
vector<int> path; | |
void backtracking (vector<int>& nums, vector<bool>& used) { | |
// 此时说明找到了一组 | |
if (path.size() == nums.size()) { | |
result.push_back(path); | |
return; | |
} | |
for (int i = 0; i < nums.size(); i++) { | |
//used [i - 1] == true,说明同一树枝 nums [i - 1] 使用过 | |
//used [i - 1] == false,说明同一树层 nums [i - 1] 使用过 | |
// 如果同一树层 nums [i - 1] 使用过则直接跳过 | |
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) { | |
continue; | |
} | |
if (used[i] == false) { | |
used[i] = true; | |
path.push_back(nums[i]); | |
backtracking(nums, used); | |
path.pop_back(); | |
used[i] = false; | |
} | |
} | |
} | |
public: | |
vector<vector<int>> permuteUnique(vector<int>& nums) { | |
result.clear(); | |
path.clear(); | |
sort(nums.begin(), nums.end()); // 排序 | |
vector<bool> used(nums.size(), false); | |
backtracking(nums, used); | |
return result; | |
} | |
}; |
# N 皇后
题目链接🔗
皇后棋子的约束条件:
- 不能同行
- 不能同列
- 不能同斜线
以 3x3 棋盘为例,将搜索过程抽象为树:
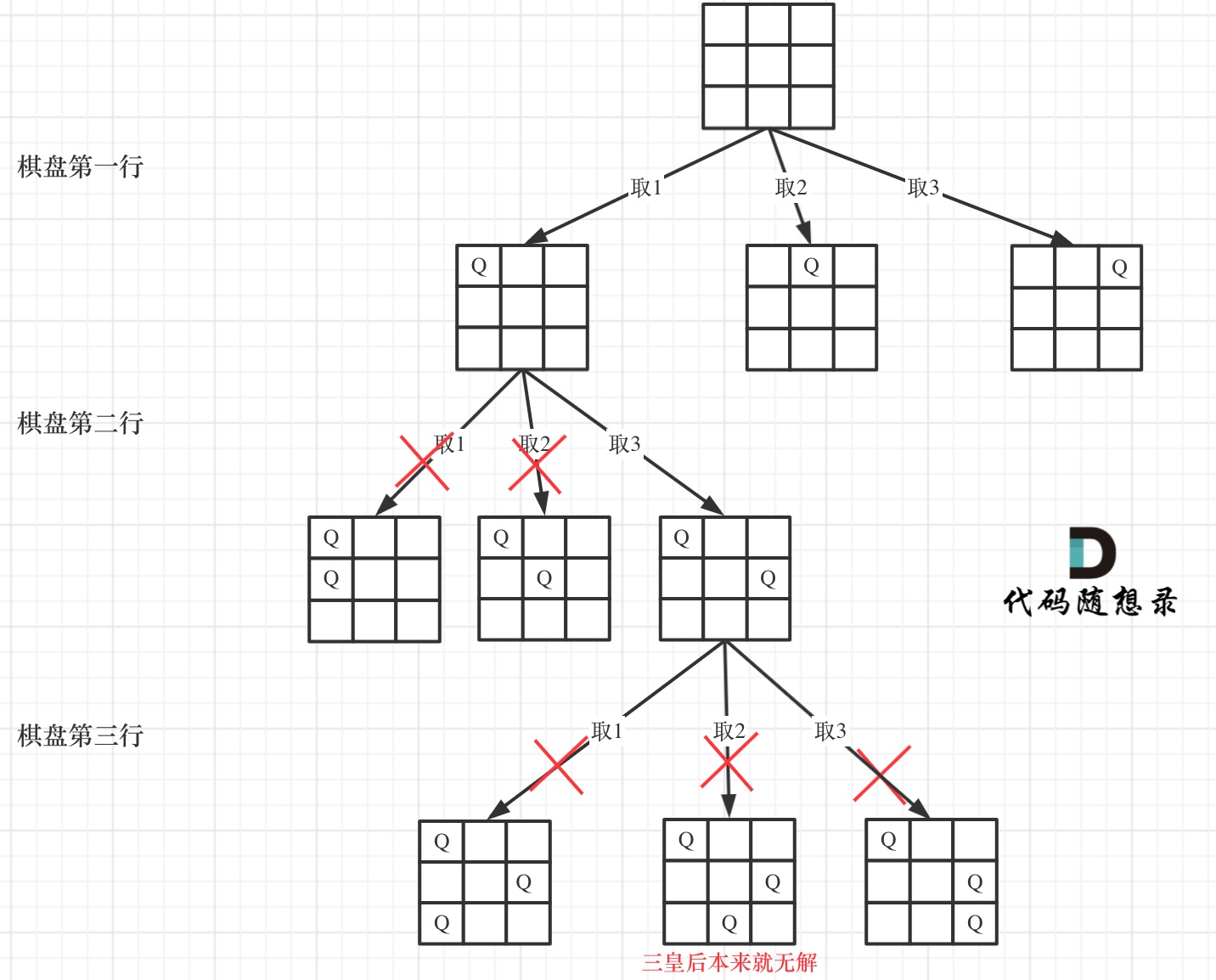
每一行每一列只放一个皇后,只需要一层 for 循环遍历一行,递归来遍历列,然后一行一列确定皇后的唯一位置。
可以看出二维矩阵的高就是树的高度,矩阵的宽就是树的宽度。
那么我们用皇后们的约束条件,来回溯搜索这棵树,只要搜索到了树的叶子节点,说明就找到了皇后们的合理位置了。
- 回溯函数参数和返回值
定义全局变量 result 来记录结果。
参数 n 是棋盘的大小,然后用 row 来记录当前遍历到棋盘的第几层了。
- 终止条件
到棋盘最底层也就是叶子节点的时候,就就可以收集结果并返回了。
- 单层搜索逻辑
递归深度就是 row 控制棋盘的行,每一层里 for 循环的 col 控制棋盘的列,一行一列,确定了放置皇后的位置。
每次都是要从新的一行的起始位置开始搜,所以都是从 0 开始。
class Solution { | |
private: | |
vector<vector<string>> result; | |
//n 为输入的棋盘大小 | |
//row 是当前递归到棋盘的第几行了 | |
void backtracking(int n, int row, vector<string>& chessboard) { | |
if (row == n) { | |
result.push_back(chessboard); | |
return; | |
} | |
for (int col = 0; col < n; col++) { | |
if (isValid(row, col, chessboard, n)) { // 验证合法就可以放 | |
chessboard[row][col] = 'Q'; // 放置皇后 | |
backtracking(n, row + 1, chessboard); | |
chessboard[row][col] = '.'; // 回溯,撤销皇后 | |
} | |
} | |
} | |
bool isValid(int row, int col, vector<string>& chessboard, int n) { | |
// 检查列 | |
for (int i = 0; i < row; i++) { // 这是一个剪枝 | |
if (chessboard[i][col] == 'Q') { | |
return false; | |
} | |
} | |
// 检查 45 度角是否有皇后 | |
for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) { | |
if (chessboard[i][j] == 'Q') { | |
return false; | |
} | |
} | |
// 检查 135 度角是否有皇后 | |
for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) { | |
if (chessboard[i][j] == 'Q') { | |
return false; | |
} | |
} | |
return true; | |
} | |
public: | |
vector<vector<string>> solveNQueens(int n) { | |
result.clear(); | |
vector<string> chessboard(n, std::string(n, '.')); | |
backtracking(n, 0, chessboard); | |
return result; | |
} | |
}; |
# 解数独
题目链接🔗
本题中二维矩阵的每一个位置都要放一个数字,并检查数字是否合法,要做一个二维递归。
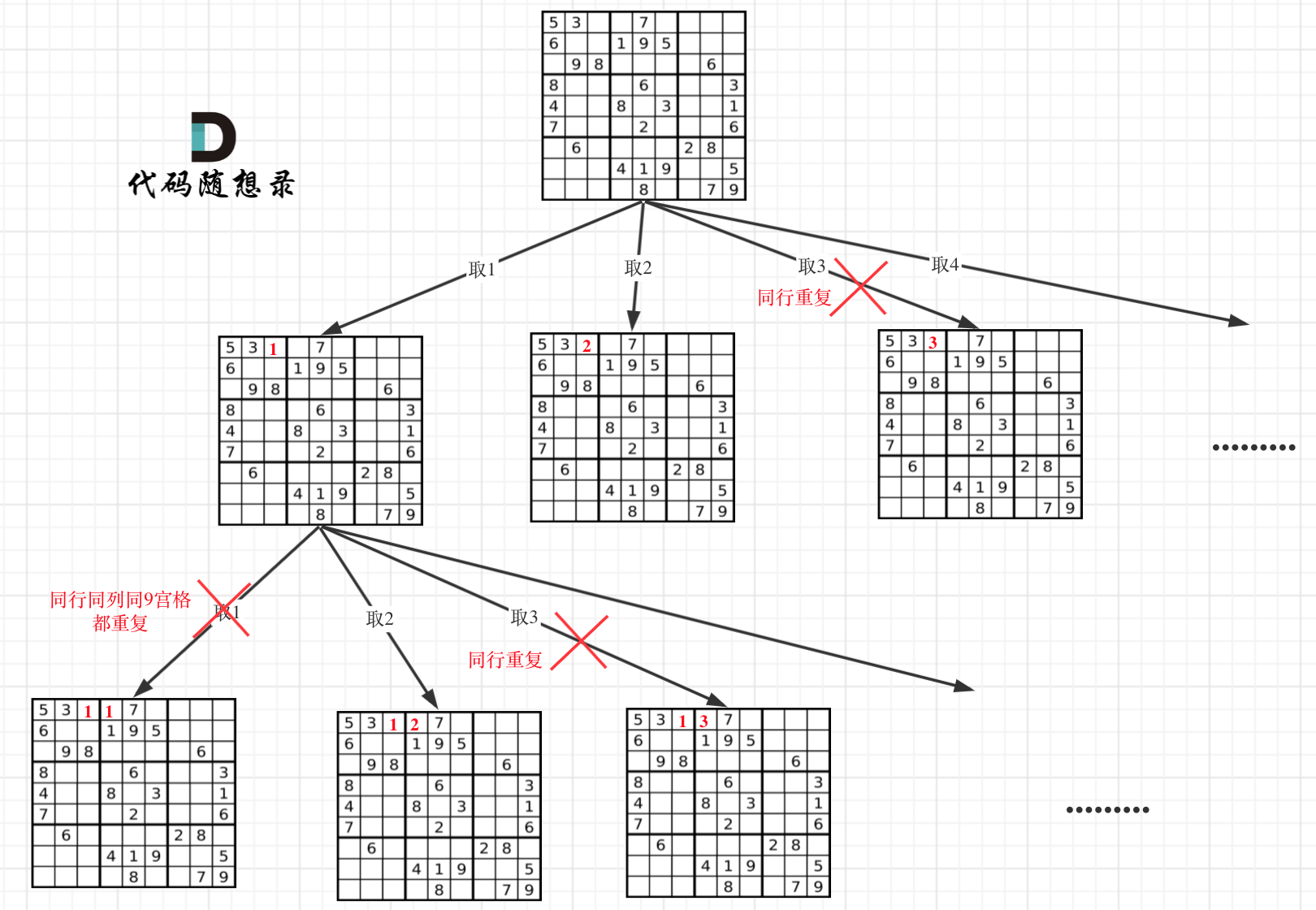
- 回溯函数参数和返回值
因为解数独找到一个符合的条件(就在树的叶子节点上)立刻就返回,相当于找从根节点到叶子节点一条唯一路径,所以需要使用 bool 返回值。
- 终止条件
本题递归不用终止条件,解数独是要遍历整个树形结构寻找可能的叶子节点就立刻返回。
- 单层搜索逻辑
因为需要做一个二维递归,一个 for 遍历行,一个 for 遍历列,一行一列确定下来之后,递归遍历这个位置放 9 个数字的可能。
如果一行一列确定下来了,这里尝试了 9 个数都不行,说明这个棋盘找不到解决数独问题的解!
那么会直接返回, 这也就是为什么没有终止条件也不会永远填不满棋盘而无限递归下去!
class Solution { | |
private: | |
bool backtracking(vector<vector<char>>& board) { | |
for (int i = 0; i < board.size(); i++) { // 遍历行 | |
for (int j = 0; j < board[0].size(); j++) { // 遍历列 | |
if (board[i][j] == '.') { | |
for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放 k 是否合适 | |
if (isValid(i, j, k, board)) { | |
board[i][j] = k; // 放置 k | |
if (backtracking(board)) return true; // 如果找到合适一组立刻返回 | |
board[i][j] = '.'; // 回溯,撤销 k | |
} | |
} | |
return false; // 9 个数都试完了,都不行,那么就返回 false | |
} | |
} | |
} | |
return true; // 遍历完没有返回 false,说明找到了合适棋盘位置了 | |
} | |
bool isValid(int row, int col, char val, vector<vector<char>>& board) { | |
for (int i = 0; i < 9; i++) { // 判断行里是否重复 | |
if (board[row][i] == val) { | |
return false; | |
} | |
} | |
for (int j = 0; j < 9; j++) { // 判断列里是否重复 | |
if (board[j][col] == val) { | |
return false; | |
} | |
} | |
int startRow = (row / 3) * 3; | |
int startCol = (col / 3) * 3; | |
for (int i = startRow; i < startRow + 3; i++) { // 判断 9 方格里是否重复 | |
for (int j = startCol; j < startCol + 3; j++) { | |
if (board[i][j] == val ) { | |
return false; | |
} | |
} | |
} | |
return true; | |
} | |
public: | |
void solveSudoku(vector<vector<char>>& board) { | |
backtracking(board); | |
} | |
}; |