# 长度最小的子数组
题目链接
# 暴力
双 for 循环,一个找起点,一个找终点。时间复杂度,超时。
class Solution { | |
public: | |
int minSubArrayLen(int target, vector<int>& nums) { | |
int result = INT32_MAX; | |
int sum = 0; // 总和 | |
int subLen = 0; // 子数组长度 | |
for(int i = 0; i < nums.size(); i++) { | |
sum = 0; | |
for(int j = i; j < nums.size(); j++) { | |
sum += nums[j]; | |
if(sum >= target) { // 一旦大于 target | |
subLen = j - i + 1; // 取长度 | |
result = result < subLen ? result : subLen; | |
break; | |
} | |
} | |
} | |
return result == INT32_MAX ? 0 : result; | |
} | |
}; |
# 滑动窗口
滑动窗口是不断调节子序列的起始位置和终止位置,从而得出结果。
如果滑动窗口用一个 for 循环,该表示起始位置还是终止位置?
- 表示起始位置的话,终止位置的确定又回到了暴力的 for 循环。因此一定是表示终止位置。
实现滑动窗口要确定如下三点:
- 窗口内的是什么
- 是满足总和 的最小连续子数组
- 如何移动窗口的起始位置
- 如果窗口内的总和大于 target,移动起始位置以缩小窗口
- 如何移动窗口的终止位置
- 为 for 循环的索引,终止条件为移动到数组最后位置
以题目中的示例来举例,s=7, 数组是 2,3,1,2,4,3,来看一下查找的过程:

滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将 暴力解法降为。
class Solution { | |
public: | |
int minSubArrayLen(int target, vector<int>& nums) { | |
int result = INT32_MAX; | |
int sum = 0; // 总和 | |
int subLen = 0; // 子数组长度 | |
int i = 0; // 窗口起始位置 | |
for(int j = 0; j < nums.size(); j++) { | |
sum += nums[j]; | |
// 使用 while 而不是 if,不断更新子序列的起始位置 | |
while(sum >= target) { | |
subLen = j - i + 1; // 取长度 | |
result = result < subLen ? result : subLen; | |
//i++:更新总和并移动滑动窗口起始位置 | |
sum -= nums[i++]; | |
} | |
} | |
return result == INT32_MAX ? 0 : result; | |
} | |
}; |
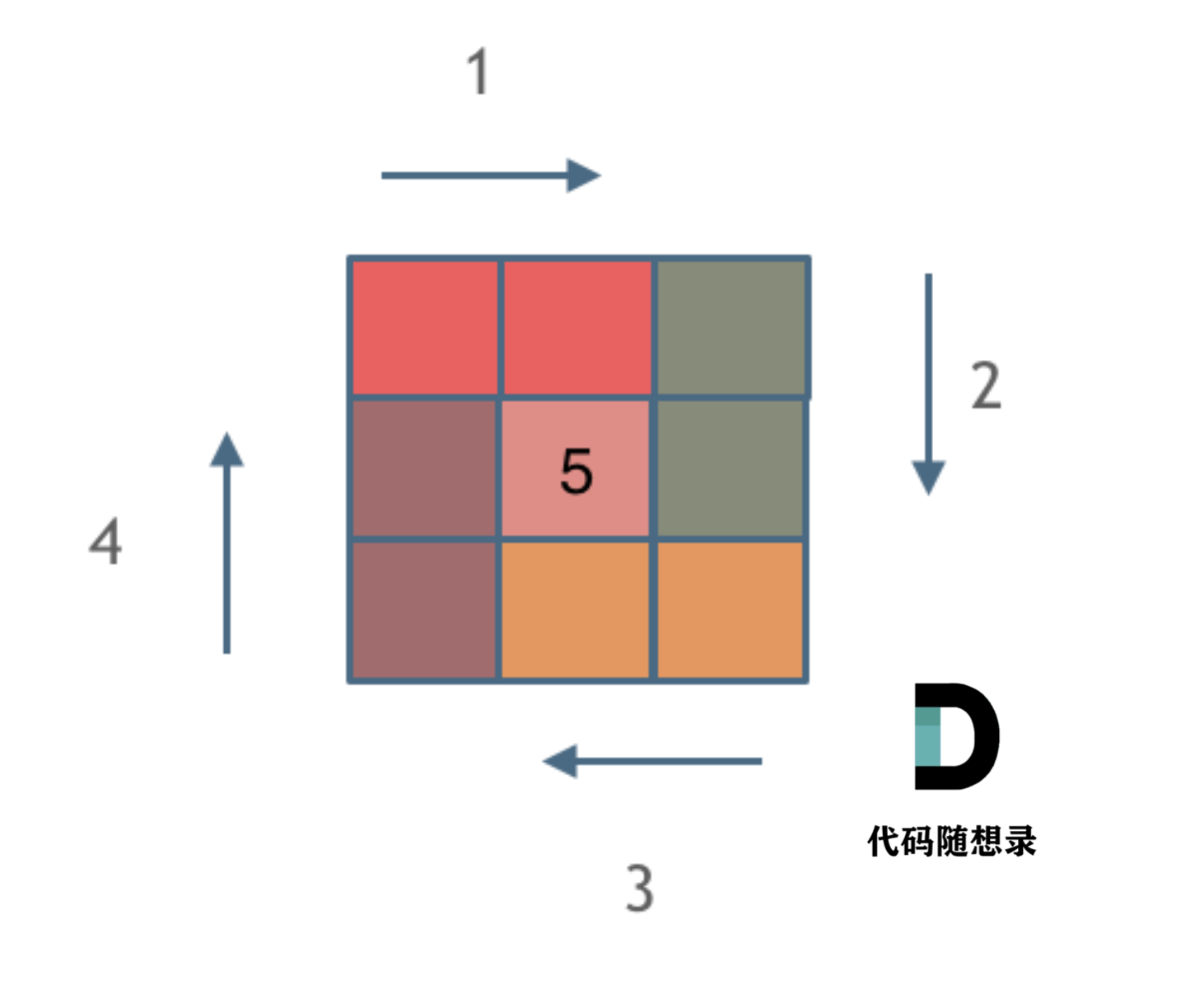
# 螺旋矩阵
题目链接
坚持循环不变量原则模拟顺时画矩阵:
- 从左到右填充上行
- 从上到下填充右列
- 从右到左填充下行
- 从下倒上填充左列
由外到内一圈圈画下去。
每画一条边都要坚持一致的左闭右开,或者左开右闭的原则,这样这一圈才能按照统一的规则画下来。
按照左闭右开的原则,来画一圈:
class Solution { | |
public: | |
vector<vector<int>> generateMatrix(int n) { | |
vector<vector<int>> res(n, vector<int>(n, 0)); | |
int startx = 0, starty = 0; // 循环起点 | |
int loop = n / 2; // 循环次数 | |
int number = 1; // 每个格子里的数值 | |
int offset = 1; // 每条边遍历的长度,每循环一次右边界收缩 1 | |
int i = 0, j = 0; | |
while(loop--) { | |
// 左闭右开模拟画一圈 | |
// 模拟从左到右填充上行 | |
for(j = starty; j < n - offset; j++) | |
res[startx][j] = number++; | |
// 模拟从上到下填充右列 | |
for(i = startx; i < n - offset; i++) | |
res[i][j] = number++; | |
// 模拟从右到左填充下行 | |
for(; j > starty; j--) | |
res[i][j] = number++; | |
// 模拟从左到右填充左列 | |
for(; i > startx; i--) | |
res[i][j] = number++; | |
// 一圈画完,下一圈起点向右下方一格移动,同时边界要收缩 | |
startx++; | |
starty++; | |
offset++; | |
} | |
//n 为奇数 单独给最中间的赋值 | |
if(n % 2 == 1) | |
res[n/2][n/2] = number; | |
return res; | |
} | |
}; |