首页 计算机科学 算法 LeetCode

# 二叉搜索树中的众数

题目链接🔗

如果不是二叉搜索树，可以将树遍历一遍，用 map 统计频率，再将 map 转化为 vector 排序，最后取前面的高频元素集合。

但二叉搜索树的中序遍历是有序的。

遍历有序数组的出现频率，从头遍历，那么一定是相邻两个元素作比较，然后就把出现频率最高的元素输出就可以了。

在树上，使用 pre 和 cur 两个指针，pre 指向前一个节点，每次 cur（当前节点）才能和 pre（前一个节点）作比较。

class Solution {
private:
    int maxCount = 0; // 最大频率
    int count = 0; // 统计频率
    TreeNode* pre = nullptr;
    vector<int> result;
    void searchBST(TreeNode* cur) {
        if (cur == nullptr) return ;
        searchBST(cur->left);       // 左
                                    // 中
        if (pre == nullptr) { // 第一个节点
            count = 1;
        } else if (pre->val == cur->val) { // 与前一个节点数值相同
            count++;
        } else { // 与前一个节点数值不同
            count = 1;
        }
        pre = cur; // 更新上一个节点
        if (count == maxCount) { // 如果和最大值相同，放进 result 中
            result.push_back(cur->val);
        }
        if (count > maxCount) { // 如果计数大于最大值频率
            maxCount = count;   // 更新最大频率
            result.clear();     // 很关键的一步，不要忘记清空 result，之前 result 里的元素都失效了
            result.push_back(cur->val);
        }
        searchBST(cur->right);      // 右
        return ;
    }
public:
    vector<int> findMode(TreeNode* root) {
        result.clear();
        searchBST(root);
        return result;
    }
};
# 二叉树的最近公共祖先
题目链接🔗
后序遍历，根据左右节点的返回值处理中间节点，自底向上查找公共祖先。
接下来就看如何判断一个节点是节点 q 和节点 p 的公共祖先呢。
首先最容易想到的一个情况：如果找到一个节点，发现左子树出现结点 p，右子树出现节点 q，或者左子树出现结点 q，右子树出现节点 p，那么该节点就是节点 p 和 q 的最近公共祖先。 即情况一：
情况一
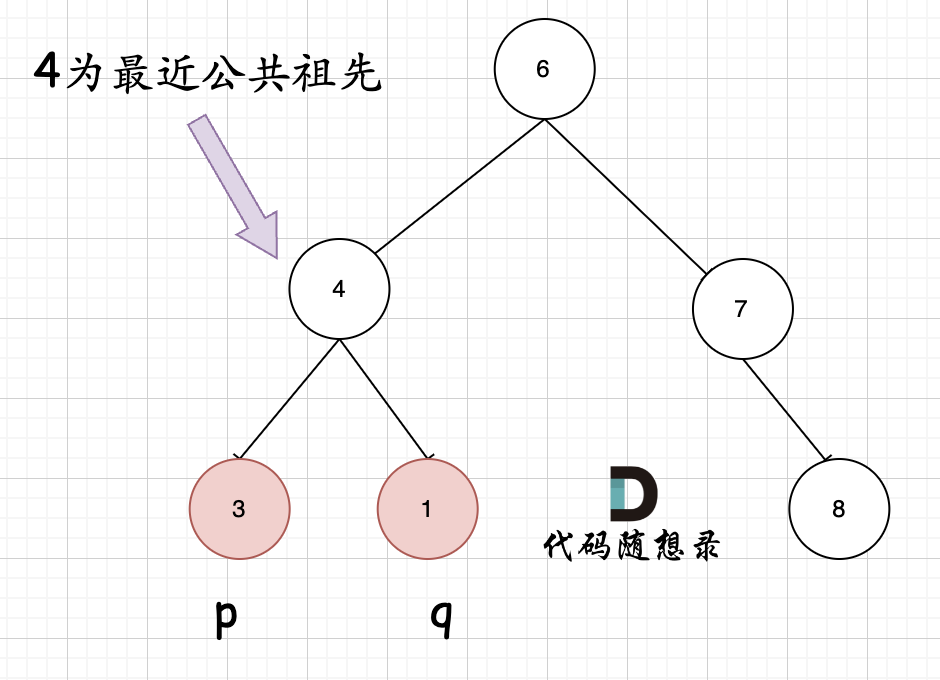
判断逻辑是 如果递归遍历遇到 q，就将 q 返回，遇到 p，就将 p 返回，如果左右子树的返回值都不为空，说明此时的中节点，一定是 q 和 p 的最近祖先。
还有一种情况，就是节点 p (或 q) 拥有一个子孙节点 q (或 p)。情况二：
情况二
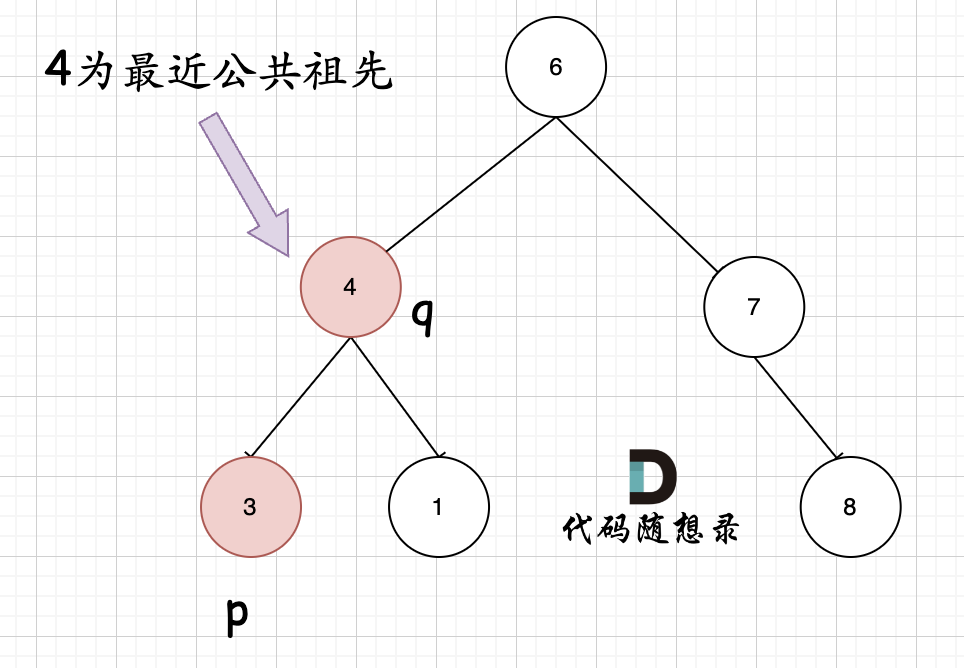
其实情况一和情况二代码实现过程都是一样的，也可以说，实现情况一的逻辑，顺便包含了情况二。
因为遇到 q 或者 p 就返回，这样也包含了 q 或者 p 本身就是 公共祖先的情况。
  1. 确定递归函数参数和返回值
利用上题目中返回值是 TreeNode * ，那么如果遇到 p 或者 q，就把 q 或者 p 返回，返回值不为空，就说明找到了 q 或者 p。
  1. 确定终止条件
遇到空的话，因为树都是空了，所以返回空。
如果root==qroot == q，或者root==proot == p，说明找到 q 或 p ，则将其返回，这个返回值，后面在中节点的处理过程中会用到。
  1. 确定单层递归逻辑
  • 如果 left 和 right 都不为空，说明此时 root 就是最近公共节点。这个比较好理解
  • 如果 left 为空，right 不为空，就返回 right，说明目标节点是通过 right 返回的，反之依然。
单层逻辑
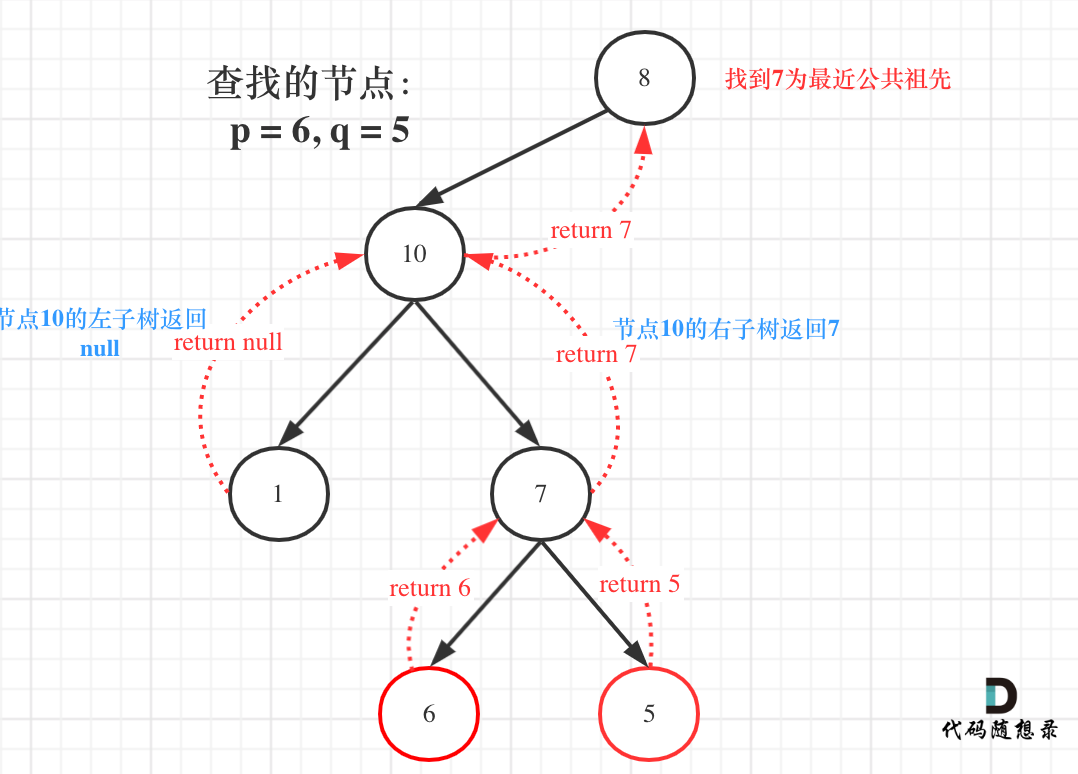
图中节点 10 的左子树返回 NULL，右子树返回的目标值是 7，那么此时节点 10 的处理逻辑就是把右子树的返回值（最近公共祖先 7）返回上去。
  • 如果 left 和 right 都为空，则返回 left 或者 right 都是可以的，也就是返回空。
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == q || root == p || root == nullptr) return root;
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        if (left != nullptr && right != nullptr) return root;
        if (left == nullptr && right != nullptr) return right;
        else if (left != nullptr && right == nullptr) return left;
        else  { //  (left == nullptr && right == nullptr)
            return nullptr;
        }
    }
};
# 二叉搜索树的最近公共祖先
题目链接🔗
二叉搜索树是有序的。
因为是有序树，所以如果中间节点是 q 和 p 的公共祖先，那么中节点的数组一定是在[p,q][p, q] 区间的。即 中节点 > p && 中节点 < q 或者 中节点 > q && 中节点 < p 。
那么只要从上到下去遍历，遇到 cur 节点是数值在[p,q][p, q] 区间中则一定可以说明该节点 cur 就是 p 和 q 的公共祖先。
在遍历二叉搜索树的时候就是寻找区间[p−>val,q−>val][p->val, q->val]（注意这里是左闭又闭）
那么如果 cur->val 大于 p->val ，同时 cur->val 大于q->val ，那么就应该向左遍历（说明目标区间在左子树上）。
需要注意的是此时不知道 p 和 q 谁大，所以两个都要判断。
如果 cur->val 小于 p->val ，同时 cur->val 小于 q->val ，那么就应该向右遍历（目标区间在右子树）。
剩下的情况，就是 cur 节点在区间 p->val <= cur->val && cur->val <= q->val 或者 q->val <= cur->val && cur->val <= p->val 中，那么 cur 就是最近公共祖先了，直接返回 cur。
# 递归
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root->val > p->val && root->val > q->val) {
            return lowestCommonAncestor(root->left, p, q);
        } else if (root->val < p->val && root->val < q->val) {
            return lowestCommonAncestor(root->right, p, q);
        } else return root;
    }
};
# 迭代
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        while(root) {
            if (root->val > p->val && root->val > q->val) {
                root = root->left;
            } else if (root->val < p->val && root->val < q->val) {
                root = root->right;
            } else return root;
        }
        return nullptr;
    }
};
# 二叉搜索树的插入操作
题目链接🔗
可以不考虑题目中提示所说的改变树的结构的插入方式。
只要按照二叉搜索树的规则去遍历，遇到空节点就插入节点就可以了。
二叉搜索树插入
# 递归
  1. 确定递归函数参数和返回值
参数就是根节点指针，以及要插入元素。
返回值的话，可以利用返回值完成新加入的节点与其父节点的赋值操作。
递归函数的返回类型为节点类型 TreeNode * 。
  1. 确定终止条件
终止条件就是找到遍历的节点为 null 的时候，就是要插入节点的位置了，并把插入的节点返回。
  1. 确定单层递归的逻辑
搜索树是有方向了，可以根据插入元素的数值，决定递归方向。
class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (root == nullptr) {
            TreeNode* node = new TreeNode(val);
            return node;
        }
        if (root->val > val) root->left = insertIntoBST(root->left, val);
        if (root->val < val) root->right = insertIntoBST(root->right, val);
        return root;
    }
};
下一层将加入节点返回，本层用 root->left 或者 root->right 将其接住，就通过递归函数返回值完成了新加入节点的父子关系赋值操作了。
# 迭代
在迭代法遍历的过程中，需要记录一下当前遍历的节点的父节点，这样才能做插入节点的操作。
class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (root == NULL) {
            TreeNode* node = new TreeNode(val);
            return node;
        }
        TreeNode* cur = root;
        TreeNode* parent = root; // 这个很重要，需要记录上一个节点，否则无法赋值新节点
        while (cur != NULL) {
            parent = cur;
            if (cur->val > val) cur = cur->left;
            else cur = cur->right;
        }
        TreeNode* node = new TreeNode(val);
        if (val < parent->val) parent->left = node;// 此时是用 parent 节点的进行赋值
        else parent->right = node;
        return root;
    }
};