# 合并二叉树

题目链接🔗

同时遍历两个树的逻辑和遍历一个树的逻辑一样，只不过传入的是两个树的节点并同时操作。

# 递归

确定递归函数的参数和返回值

传入两个树的根节点，返回的是合并后的根节点。

确定递归的终止条件

传入了两个树，那么就有两个树遍历的节点 t1 和 t2，如果 $t1 == NULL$ 了，两个树合并就应该是 t2 了（如果 t2 也为 NULL 也无所谓，合并之后就是 NULL）。

反过来如果 $t2 == NULL$ ，那么两个数合并就是 t1（如果 t1 也为 NULL 也无所谓，合并之后就是 NULL）。

确定单层递归的逻辑

重复利用 t1 或者 t2，例如 t1 就是合并之后的根节点。也可以不改变原来树的结构，新建一个根节点。

那么单层递归中就把两棵树元素加到一起。

	class Solution {
	public:
	TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
	if (t1 == nullptr) return t2; // 如果 t1 为空，合并之后就应该是 t2
	if (t2 == nullptr) return t1; // 如果 t2 为空，合并之后就应该是 t1
	// 修改了 t1 的数值和结构
	t1->val += t2->val; // 中
	t1->left = mergeTrees(t1->left, t2->left); // 左
	t1->right = mergeTrees(t1->right, t2->right); // 右
	return t1;
	}
	};

# 迭代

	class Solution {
	public:
	TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
	if (t1 == NULL) return t2;
	if (t2 == NULL) return t1;
	queue<TreeNode*> que;
	que.push(t1);
	que.push(t2);
	while(!que.empty()) {
	TreeNode* node1 = que.front(); que.pop();
	TreeNode* node2 = que.front(); que.pop();
	// 此时两个节点一定不为空，val 相加
	node1->val += node2->val;

	// 如果两棵树左节点都不为空，加入队列
	if (node1->left != NULL && node2->left != NULL) {
	que.push(node1->left);
	que.push(node2->left);
	}
	// 如果两棵树右节点都不为空，加入队列
	if (node1->right != NULL && node2->right != NULL) {
	que.push(node1->right);
	que.push(node2->right);
	}

	// 当 t1 的左节点为空 t2 左节点不为空，就赋值过去
	if (node1->left == NULL && node2->left != NULL) {
	node1->left = node2->left;
	}
	// 当 t1 的右节点为空 t2 右节点不为空，就赋值过去
	if (node1->right == NULL && node2->right != NULL) {
	node1->right = node2->right;
	}
	}
	return t1;
	}
	};

# 二叉搜索树中的搜索

题目链接🔗

二叉搜索树是一个有序树：

若它的左子树不空，则左子树上的所有节点的值均小于根节点的值。
若它的右子树不空，则右子树上的所有节点的值均小于根节点的值。
左右子树也分别为二叉搜索树。

# 递归

确定递归函数的参数和返回值

参数是根节点和要搜索的值，返回值是这个搜索值所在的节点。

确定递归终止条件

如果正在搜索的节点为空或者找到搜索值了，就返回节点。

确定单层递归的逻辑

如果 $root->val > val$ ，搜索左子树，如果 $root->val < val$ ，就搜索右子树，最后如果都没有搜索到，就返回 NULL。

	class Solution {
	public:
	TreeNode* searchBST(TreeNode* root, int val) {
	if (root == nullptr \|\| root->val == val) return root;
	if (root->val > val) return searchBST(root->left, val);
	if (root->val < val) return searchBST(root->right, val);
	return nullptr;
	}
	};

# 迭代

因为二叉搜索树的有序性，可以不借助辅助栈或队列，并且不需要回溯，因为查找的方向已经决定好了。

	class Solution {
	public:
	TreeNode* searchBST(TreeNode* root, int val) {
	while (root != nullptr) {
	if (root->val > val) root = root->left;
	else if (root->val < val) root = root->right;
	else return root;
	}
	return nullptr;
	}
	};

# 验证二叉搜索树

题目链接🔗

中序遍历下次，输出的二叉搜索树节点的数值是有序序列。

基于此特性，验证二叉搜索树就相当于变成了判断一个序列是不是递增的了。

# 递归法

把二叉树转化为数组。

	class Solution {
	private:
	vector<int> vec;
	void traversal(TreeNode* root) {
	if (root == nullptr) return;
	traversal(root->left);
	vec.push_back(root->val); // 将二叉搜索树转换为有序数组
	traversal(root->right);
	}
	public:
	bool isValidBST(TreeNode* root) {
	vec.clear(); // 不加这句在 leetcode 上也可以过，但最好加上
	traversal(root);
	for (int i = 1; i < vec.size(); i++) {
	// 注意要小于等于，搜索树里不能有相同元素
	if (vec[i] <= vec[i - 1]) return false;
	}
	return true;
	}
	};

在递归遍历的过程中判断是否有序。

	class Solution {
	public:
	TreeNode* pre = nullptr; // 用来记录前一个节点
	bool isValidBST(TreeNode* root) {
	if (root == nullptr) return true;
	bool left = isValidBST(root->left);

	if (pre != nullptr && pre->val >= root->val) return false;
	pre = root; // 记录前一个节点

	bool right = isValidBST(root->right);
	return left && right;
	}
	};

# 迭代法

用栈模拟二叉树的中序遍历。

	class Solution {
	public:
	bool isValidBST(TreeNode* root) {
	stack<TreeNode*> st;
	TreeNode* cur = root;
	TreeNode* pre = nullptr; // 记录前一个节点
	while (cur != nullptr \|\| !st.empty()) {
	if (cur != nullptr) {
	st.push(cur);
	cur = cur->left; // 左
	} else {
	cur = st.top(); // 中
	st.pop();
	if (pre != nullptr && cur->val <= pre->val)
	return false;
	pre = cur; // 保存前一个访问的结点

	cur = cur->right; // 右
	}
	}
	return true;
	}
	};

# 二叉搜索树的最小绝对差

题目链接🔗

二叉搜索树可是有序的。

遇到在二叉搜索树上求最值、差值之类的，就把它想成在一个有序数组上求最值，求差值。

# 递归

二叉搜索树转换成有序数组，然后遍历一遍数组，就统计出来最小差值了。

	class Solution {
	private:
	vector<int> vec;
	void traversal(TreeNode* root) {
	if (root == nullptr) return;
	traversal(root->left);
	vec.push_back(root->val); // 将二叉搜索树转换为有序数组
	traversal(root->right);
	}
	public:
	int getMinimumDifference(TreeNode* root) {
	vec.clear();
	traversal(root);
	if (vec.size() < 2) return 0;
	int result = INT_MAX;
	for (int i = 1; i < vec.size(); i++) { // 统计有序数组的最小差值
	result = min(result, vec[i] - vec[i-1]);
	}
	return result;
	}
	};

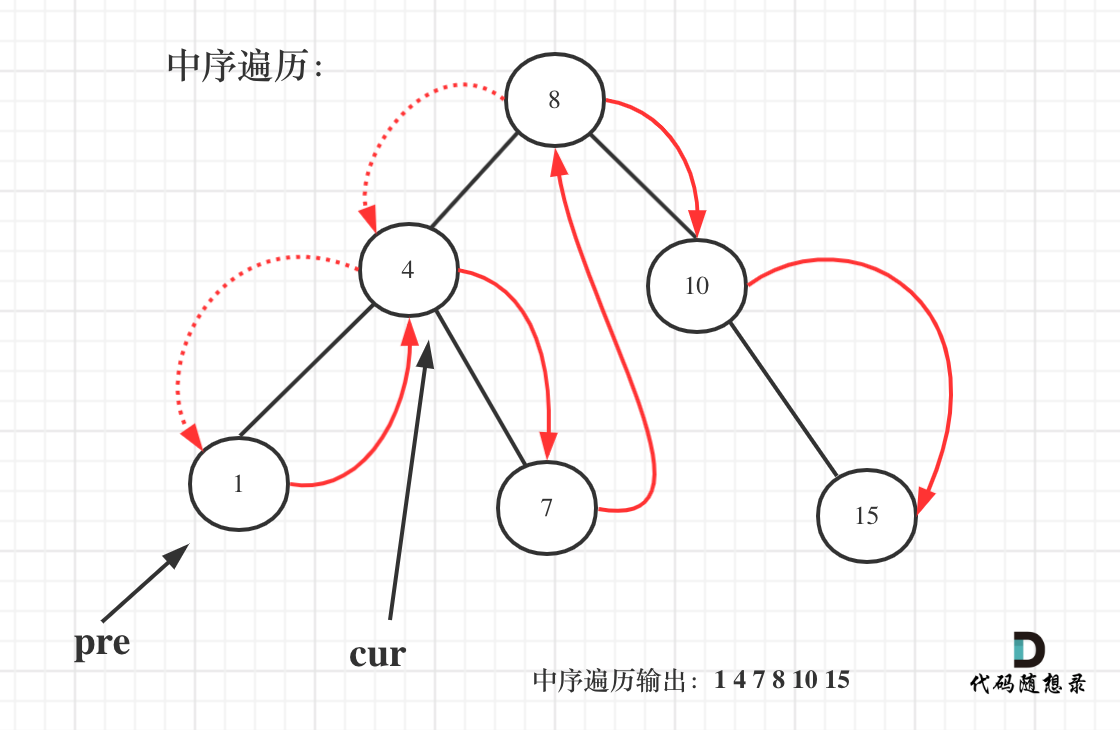
遍历过程中直接计算，需要用一个 pre 记录 cur 的前一个节点。

求二叉搜索树的最小绝对差

	class Solution {
	private:
	int result = INT_MAX;
	TreeNode* pre = nullptr;
	void traversal(TreeNode* cur) {
	if (cur == nullptr) return;
	traversal(cur->left); // 左
	if (pre != nullptr){ // 中
	result = min(result, cur->val - pre->val);
	}
	pre = cur; // 记录前一个
	traversal(cur->right); // 右
	}
	public:
	int getMinimumDifference(TreeNode* root) {
	traversal(root);
	return result;
	}
	};

# 迭代法

	class Solution {
	public:
	int getMinimumDifference(TreeNode* root) {
	stack<TreeNode*> st;
	TreeNode* cur = root;
	TreeNode* pre = nullptr;
	int result = INT_MAX;
	while (cur != nullptr \|\| !st.empty()) {
	if (cur != nullptr) { // 指针来访问节点，访问到最底层
	st.push(cur); // 将访问的节点放进栈
	cur = cur->left; // 左
	} else {
	cur = st.top();
	st.pop();
	if (pre != nullptr) { // 中
	result = min(result, cur->val - pre->val);
	}
	pre = cur;
	cur = cur->right; // 右
	}
	}
	return result;
	}
	};

二叉树 LeetCode 递归广度优先遍历深度优先遍历二叉搜索树

# 合并二叉树

# 递归

# 迭代

# 二叉搜索树中的搜索

# 递归

# 迭代

# 验证二叉搜索树

# 递归法

# 迭代法

# 二叉搜索树的最小绝对差

# 递归

# 迭代法

【代码随想录Day15】二叉树 Part.4

【代码随想录Day17】二叉树 Part.6