# 栈与队列理论基础

队列是先进先出，栈是先进后出。

栈与队列

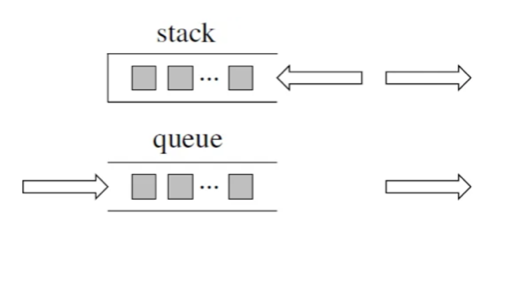
栈提供 push 和 pop 等接口，所有元素必须符合先进后出的规则，所以栈不提供走访功能和迭代器。

栈以底层容器来完成所有工作，对外统一接口，底层容器是可插拔的。

因此在 STL 中栈汪汪不被归为容器 (container)，而被归为容器适配器 (container adapter)。

栈的底层实现可以是 vector ， deque ， list 等数组和链表的底层实现。

常用的 SGI STL 如果没有指定底层实现，默认是以 deque 为底层数据结构。

deque 是一个双向队列，只要封住一段，开通一段就可以实现栈的逻辑。

队列和栈的特性是基本一致的，同样不允许有遍历行为，不提供迭代器，SGI STL 中队列一样以 deque 为缺省情况下的底层数据结构。

# 用栈实现队列

题目链接🔗

使用栈来模拟队列需要用到两个栈，一个输出栈，一个输入栈。

	class MyQueue {
	private:
	stack<int> stIn;
	stack<int> stOut;
	public:
	MyQueue() {}

	void push(int x) {
	stIn.push(x);
	}

	int pop() {
	// 输出栈为空，移入输入栈所有数据
	if(stOut.empty()){
	while(!stIn.empty()) {
	stOut.push(stIn.top());
	stIn.pop();
	}
	}
	int tmp = stOut.top();
	stOut.pop();
	return tmp;
	}

	int peek() {
	int tmp = this->pop(); // 调用已有的 pop ()
	stOut.push(tmp); // 弹出了要再添加回去
	return tmp;
	}

	bool empty() {
	return stIn.empty() && stOut.empty();
	}
	};

题目链接🔗

队列是先进先出的规则，把一个队列元素移入另一个队列，数据的顺序没有改变。

两个队列实现栈

两个队列中有一个队列的作用是备份。que1 队列中除最后一个元素以外的所有元素全部移入 que2，弹出 que1 最后的元素，再将 que2 的元素全部移回 que1

	class MyStack {
	public:
	queue<int> que1;
	queue<int> que2; // 辅助队列，用来备份
	/** Initialize your data structure here. */
	MyStack() {}

	/** Push element x onto stack. */
	void push(int x) {
	que1.push(x);
	}

	/** Removes the element on top of the stack and returns that element. */
	int pop() {
	int size = que1.size();
	size--;
	while (size--) { // 将 que1 导入 que2，但要留下最后一个元素
	que2.push(que1.front());
	que1.pop();
	}

	int result = que1.front(); // 留下的最后一个元素就是要返回的值
	que1.pop();
	que1 = que2; // 再将 que2 赋值给 que1
	while (!que2.empty()) { // 清空 que2
	que2.pop();
	}
	return result;
	}

	/** Get the top element. */
	int top() {
	return que1.back();
	}

	/** Returns whether the stack is empty. */
	bool empty() {
	return que1.empty();
	}
	};

一个队列在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素外）重新添加到队列尾部，此时再去弹出元素就是栈的顺序了。

	class MyStack {
	public:
	queue<int> que;
	/** Initialize your data structure here. */
	MyStack() {

	}
	/** Push element x onto stack. */
	void push(int x) {
	que.push(x);
	}
	/** Removes the element on top of the stack and returns that element. */
	int pop() {
	int size = que.size();
	size--;
	while (size--) { // 将队列头部的元素（除了最后一个元素外）重新添加到队列尾部
	que.push(que.front());
	que.pop();
	}
	int result = que.front(); // 此时弹出的元素顺序就是栈的顺序了
	que.pop();
	return result;
	}

	/** Get the top element. */
	int top() {
	return que.back();
	}

	/** Returns whether the stack is empty. */
	bool empty() {
	return que.empty();
	}
	};

题目链接🔗

括号匹配是栈的经典题目。

首先分析一下几种不匹配的情况：

只要代码覆盖三种不匹配的情况，基本不会出现问题。

匹配括号

当字符串遍历完之后，栈是空的，就说明全都匹配了。

	class Solution {
	public:
	bool isValid(string s) {
	if (s.size() % 2 != 0) return false; // 如果 s 的长度为奇数，一定不符合要求
	stack<char> st;
	for (int i = 0; i < s.size(); i++) {
	if (s[i] == '(') st.push(')');
	else if (s[i] == '{') st.push('}');
	else if (s[i] == '[') st.push(']');
	// 第三种情况：遍历字符串匹配的过程中，栈已经为空了，没有匹配的字符了，说明右括号没有找到对应的左括号 return false
	// 第二种情况：遍历字符串匹配的过程中，发现栈里没有我们要匹配的字符。所以 return false
	else if (st.empty() \|\| st.top() != s[i]) return false;
	else st.pop(); //st.top () 与 s [i] 相等，栈弹出元素
	}
	// 第一种情况：此时我们已经遍历完了字符串，但是栈不为空，说明有相应的左括号没有右括号来匹配，所以 return false，否则就 return true
	return st.empty();
	}
	};

在匹配左括号的时候，右括号先入栈，就只需要比较当前元素和栈顶相不相等就可以了，比左括号先入栈代码实现要简单