Weekly Contest 2 - UM ICPC Training Group - ACM - 算法 - 计算机科学

# 头文件

	#include <iostream>
	#include <cstdio>
	#include <cstdlib>
	#include <cstring>
	#include <algorithm>
	#include<functional>
	#include <cmath>
	#include <ctime>
	#include <queue>
	#include <set>
	#include <sstream>
	#include <unordered_set>
	#include <map>
	#include <unordered_map>
	#include <vector>
	#include <stack>
	#include <regex>
	using namespace std;
	const int INF = 0x3f3f3f3f;
	const int maxn = 1e3 + 5;
	const int MOD = 1e9 + 7;

	using namespace std;

# A - Chinese Zodiac

The Chinese Zodiac, known as Sheng Xiao, is based on a twelve-year cycle, each year in the cycle related to an animal sign. These signs are the rat, ox, tiger, rabbit, dragon, snake, horse, sheep, monkey, rooster, dog and pig.
Victoria is married to a younger man, but no one knows the real age difference between the couple. The good news is that she told us their Chinese Zodiac signs. Their years of birth in luner calendar is not the same. Here we can guess a very rough estimate of the minimum age difference between them.
If, for instance, the signs of Victoria and her husband are ox and rabbit respectively, the estimate should be 2 years. But if the signs of the couple is the same, the answer should be 12 years.

Input
The first line of input contains an integer $T~(1\le T\le 1000)$ indicating the number of test cases.
For each test case a line of two strings describes the signs of Victoria and her husband.

Output
For each test case output an integer in a line.

Sample

模拟题。用 map 代码量更少。

	int main() {
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	int T;
	string signs[12] = { "rat", "ox", "tiger", "rabbit", "dragon", "snake", "horse", "sheep", "monkey", "rooster", "dog", "pig"};
	string a,b;
	cin >> T;
	while(T--) {
	cin >> a >> b;
	int x, y;
	for(int i = 0; i < 12; i++){
	if(signs[i] == a)
	x = i;
	if(signs[i] == b)
	y = i;
	}
	if(x == y)
	cout << 12 << endl;
	else if(x - y > 0)
	cout << 12 - (x - y) << endl;
	else
	cout << y - x << endl;
	}
	return 0;
	}

# B - Count Color

Chosen Problem Solving and Program design as an optional course, you are required to solve all kinds of problems. Here, we get a new problem.
There is a very long board with length L centimeter, L is a positive integer, so we can evenly divide the board into L segments, and they are labeled by 1, 2, ... L from left to right, each is 1 centimeter long. Now we have to color the board - one segment with only one color. We can do following two operations on the board:

"C A B C" Color the board from segment A to segment B with color C.
"P A B" Output the number of different colors painted between segment A and segment B (including).
In our daily life, we have very few words to describe a color (red, green, blue, yellow…), so you may assume that the total number of different colors T is very small. To make it simple, we express the names of colors as color 1, color 2, ... color T. At the beginning, the board was painted in color 1. Now the rest of problem is left to your.

Input
First line of input contains L (1 <= L <= 100000), T (1 <= T <= 30) and O (1 <= O <= 100000). Here O denotes the number of operations. Following O lines, each contains "C A B C" or "P A B" (here A, B, C are integers, and A may be larger than B) as an operation defined previously.

Output
Ouput results of the output operation in order, each line contains a number.

Sample

线段树 + 位运算 + lazy 思想。对于区间的颜色数用一个 32 位整数保存，该整数的二进制位每一位表示是否包含该颜色，对两个整数的或运算可以求这两个集合的并。

	#define lson l,m,rt<<1
	#define rson m+1,r,rt<<1\|1
	const int N = 1000005;
	int sum[N << 2], flag[N << 2];

	void push_up(int rt) {
	sum[rt] = sum[rt << 1] \| sum[rt << 1 \| 1];
	}

	void build(int l, int r, int rt) {
	sum[rt] = 1;
	if (l == r)return;
	int m = (l + r) >> 1;
	build(lson);
	build(rson);
	}

	void push_down(int rt) {
	if (flag[rt]) {
	int C = flag[rt];
	flag[rt << 1] = C;
	flag[rt << 1 \| 1] = C;
	sum[rt << 1] = 1 << (C - 1);
	sum[rt << 1 \| 1] = 1 << (C - 1);
	flag[rt] = 0;
	}
	}

	void update(int L, int R, int C, int l, int r, int rt) {
	if (L <= l && r <= R) {
	sum[rt] = 1 << (C - 1);
	flag[rt] = C;
	return;
	}
	int m = (l + r) >> 1;
	push_down(rt);
	if (L <= m)update(L, R, C, lson);
	if (R > m)update(L, R, C, rson);
	push_up(rt);
	}

	int query(int L, int R, int l, int r, int rt) {
	if (L <= l && r <= R) {
	return sum[rt];
	}
	int m = (l + r) >> 1;
	push_down(rt);
	int ans = 0;
	if (L <= m)ans \|= query(L, R, lson);
	if (R > m)ans \|= query(L, R, rson);
	return ans;
	}

	int main() {
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	int n, T, O, a, b, c;
	scanf("%d %d %d", &n, &T, &O);
	char s[5];
	build(1, n, 1);
	memset(flag, 0, sizeof(flag));
	while (O--) {
	scanf("%s", s);
	if (s[0] == 'C') {
	scanf("%d %d %d", &a, &b, &c);
	if (a > b)swap(a, b);
	update(a, b, c, 1, n, 1);
	} else {
	scanf("%d %d", &a, &b);
	if (a > b)swap(a, b);
	int tmp = query(a, b, 1, n, 1);
	int res = 0;
	while (tmp) {
	if (tmp & 1)res++;
	tmp >>= 1;
	}
	printf("%d\n", res);
	}
	}
	return 0;
	}

# C - Stealing Harry Potter's Precious

Harry Potter has some precious. For example, his invisible robe, his wand and his owl. When Hogwarts school is in holiday, Harry Potter has to go back to uncle Vernon's home. But he can't bring his precious with him. As you know, uncle Vernon never allows such magic things in his house. So Harry has to deposit his precious in the Gringotts Wizarding Bank which is owned by some goblins. The bank can be considered as a N × M grid consisting of N × M rooms. Each room has a coordinate. The coordinates of the upper-left room is (1,1) , the down-right room is (N,M) and the room below the upper-left room is (2,1)..... A 3×4 bank grid is shown below:

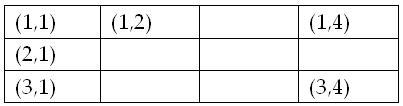
Some rooms are indestructible and some rooms are vulnerable. Goblins always care more about their own safety than their customers' properties, so they live in the indestructible rooms and put customers' properties in vulnerable rooms. Harry Potter's precious are also put in some vulnerable rooms. Dudely wants to steal Harry's things this holiday. He gets the most advanced drilling machine from his father, uncle Vernon, and drills into the bank. But he can only pass though the vulnerable rooms. He can't access the indestructible rooms. He starts from a certain vulnerable room, and then moves in four directions: north, east, south and west. Dudely knows where Harry's precious are. He wants to collect all Harry's precious by as less steps as possible. Moving from one room to another adjacent room is called a 'step'. Dudely doesn't want to get out of the bank before he collects all Harry's things. Dudely is stupid.He pay you $1,000,000 to figure out at least how many steps he must take to get all Harry's precious.

Input
There are several test cases.
In each test cases:
The first line are two integers N and M, meaning that the bank is a N × M grid(0<N,M <= 100).
Then a N×M matrix follows. Each element is a letter standing for a room. '#' means a indestructible room, '.' means a vulnerable room, and the only '@' means the vulnerable room from which Dudely starts to move.
The next line is an integer K ( 0 < K <= 4), indicating there are K Harry Potter's precious in the bank.
In next K lines, each line describes the position of a Harry Potter's precious by two integers X and Y, meaning that there is a precious in room (X,Y).
The input ends with N = 0 and M = 0

Output
For each test case, print the minimum number of steps Dudely must take. If Dudely can't get all Harry's things, print -1.

Sample

BFS + 全排列。

	char grid[105][105]; // 棋盘
	bool visit[105][105]; // 这个点是否访问过
	int d[105][105]; // 两点之间的最小距离
	int px[4] = {0, 0 ,1, -1};
	int py[4] = {1, -1 ,0, 0};
	int n, m, k;

	struct node {
	int x, y;
	int step;
	}p[5];

	void init() {
	memset(grid, 0, sizeof(grid));
	for(int i = 1; i <= n; i++) {
	scanf("%s", grid[i] + 1);
	for(int j = 1; j <= m; j++) {
	if(grid[i][j] == '@'){
	p[0].x = i;
	p[0].y = j;
	}
	}
	}
	scanf("%d", &k);
	for(int i = 1; i <= k; i++)
	scanf("%d %d", &p[i].x, &p[i].y);
	}

	int BFS(node st, node en) {
	queue<node> q;
	memset(visit, 0, sizeof(visit));
	visit[st.x][st.y] = 1;
	st.step = 0;
	q.push(st);
	while(!q.empty()){
	node now, next;
	now = q.front();
	q.pop();
	if(now.x == en.x && now.y == en.y){
	return now.step;
	}
	for(int i = 0; i < 4; i++){
	next.x = now.x + px[i];
	next.y = now.y + py[i];
	if(next.x > 0 && next.x <= n && next.y > 0 && next.y <= n && !visit[next.x][next.y] && grid[next.x][next.y]!='#'){
	visit[next.x][next.y] = 1;
	next.step = now.step + 1;
	q.push(next);
	}
	}
	}
	return -1;
	}

	bool judge(){
	memset(d, 0, sizeof(d));
	for(int i = 0; i <= k; i++){
	for (int j = i + 1; j <= k; ++j) {
	int dis = BFS(p[i], p[j]);
	if(dis == -1) return false;
	d[i][j] = d[j][i] = dis;
	}
	}
	return true;
	}

	int solve(){
	int a[105], ans = INF;
	for(int i = 0; i <= k; i++){
	a[i] = i;
	}
	do{
	int sum = 0;
	for(int i = 0; i < k; i++){
	sum += d[a[i]][a[i + 1]];
	}
	ans = min(sum, ans);
	}while(next_permutation(a + 1, a + 1 + k));
	return ans;
	}

	int main()
	{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	while(scanf("%d %d", &n, &m) && (n \|\| m)){
	init();
	if(judge())
	printf("%d\n", solve());
	else
	printf("-1\n");
	}
	return 0;
	}

# D - Football

Consider a single-elimination football tournament involving $$2^n teams, denoted $1,2,\cdot\cdot\cdot,2^n$ . In each round of the tournament, all teams still in the tournament are placed in a list in order of increasing index. Then, the first team in the list plays the second team, the third team plays the fourth team, etc. The winners of these matches advance to the next round, and the losers are eliminated. After n rounds, only one team remains undefeated; this team is declared the winner.

Given a matrix $P = [p_{ij}]$ such that $p_{ij}$ is the probability that team $i$ will beat team $j$ in a match determine which team is most likely to win the tournament.

Input
The input test file will contain multiple test cases. Each test case will begin with a single line containing $n~(1 \leq n \leq 7)$ The next $2^n$ lines each contain $2^n$ values; here, the jth value on the ith line represents $p_{ij}$ . The matrix $P$ will satisfy the constraints that $p_{ij} = 1 - p_{ji}$ for all $i \neq j$ and $p_{ii} = 0.0$ for all $i$ . The end-of-file is denoted by a single line containing the number −1. Note that each of the matrix entries in this problem is given as a floating-point value. To avoid precision problems, make sure that you use either the double data type instead of float.

Output
The output file should contain a single line for each test case indicating the number of the team most likely to win. To prevent floating-point precision issues, it is guaranteed that the difference in win probability for the top two teams will be at least 0.01.

Constraints

Sample

概率 DP + 位运算。 $dp[i][j]$ 表示第 $i$ 场比赛第 $j$ 队获胜概率，状态转移方程为 $dp[i][j] +=dp[i-1][j]*dp[i-1][k]*p[j][k]$ 。注意两队相邻时才能比赛：每轮淘汰一半的队伍，所以可以右移一位操作；异或（XOR）1 有个特性，可以让偶数 + 1，奇数 - 1，利用这个特性可以判断两队是否相邻。

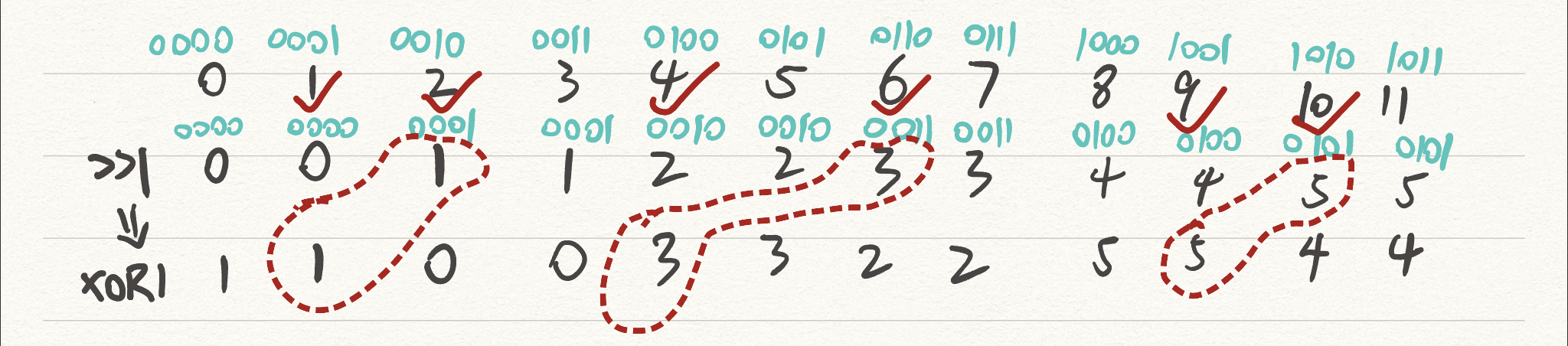
举个例子，上图中打对钩的队伍在第一轮获胜进入第二轮，用红色虚线框出的就是第二轮比赛的队伍。

	double dp[200][200], p[200][200];

	int main()
	{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	int n;
	while(cin >> n) {
	if(n == -1) break;
	int num = 1 << n;
	memset(dp, 0, sizeof(dp));
	for(int i = 0; i < num; i++){
	for(int j = 0; j < num; j++){
	cin >> p[i][j];
	}
	}
	for(int i = 0; i < num; i++)
	dp[0][i] = 1;
	for(int i = 1; i <= n; i++) {
	for(int j = 0; j < num; j++) {
	int x = (j >> (i-1))^1;
	// cout << "i = "<< i << "j = "<< j << x <<endl;
	for(int k = 0; k < num; k++) {
	// cout << "i = "<< i << "j = "<< j << "k = " << k << (k >> (i-1)) <<endl;
	if(((j >> (i-1))^1) == (k >> (i-1))){
	dp[i][j] += dp[i-1][j] * dp[i-1][k] * p[j][k];
	}
	}
	}
	}
	int ans = 0;
	for(int i = 0; i < num; i++){
	if(dp[n][i] > dp[n][ans])
	ans = i;
	}
	cout << ans+1 << endl;
	}
	return 0;
	}

# E - Graph Game

目测博弈论，待补充（摆了）。

# F - Hard Code

Some strange code is sent to Da Shan High School. It's said to be the prophet's note. The note is extremely hard to understand. However, Professor Meng is so smart that he successfully found the pattern of the code. That is, the length of the code is the product of two prime numbers. He tries to reallocate the code into a grid of size N*M, where M is the bigger prime. In specific, he writes down the letters of the code to the cells one by one, from left to right, and from top to button. In this way, he found the code eventually readable.
Professor Meng wants to know all the secrets of the note right now. But he doesn't take his computer with him. Can you help him?

Input
The first line of the input is $L~(L \leq 1000)$ , which means the number of test cases.
For each test case, the first line contains two prime numbers, which indicates $N, M~(0 < N*M \leq 1000)$ as describe above. The second line contains a string, i.e., the code, containing only lowercase letters. It’s guaranteed the length of the string equals to N * M.

Output
For each test case, output N lines, each line with M letters representing the readable code after the reallocation.

Sample

模拟题。字符串分割。

	int main(){
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	int L, n, m;
	string s;
	cin >> L;
	while(L--) {
	res.clear();
	cin >> n >> m;
	cin >> s;
	for(int i = 0; i < s.size(); i++) {
	cout << s[i];
	if((i + 1) % m == 0)
	cout << endl;
	}
	}
	return 0;
	}

# G - Hard Disk Drive

Yesterday your dear cousin Coach Pang gave you a new 100MB hard disk drive (HDD) as a gift because you will get married next year.
But you turned on your computer and the operating system (OS) told you the HDD is about 95MB. The 5MB of space is missing. It is known that the HDD manufacturers have a different capacity measurement. The manufacturers think 1 “kilo” is 1000 but the OS thinks that is 1024. There are several descriptions of the size of an HDD. They are byte, kilobyte, megabyte, gigabyte, terabyte, petabyte, exabyte, zetabyte and yottabyte. Each one equals a “kilo” of the previous one. For example 1 gigabyte is 1 “kilo” megabytes.
Now you know the size of a hard disk represented by manufacturers and you want to calculate the percentage of the “missing part”.

Input
The first line contains an integer T, which indicates the number of test cases.
For each test case, there is one line contains a string in format “number[unit]” where number is a positive integer within [1, 1000] and unit is the description of size which could be “B”, “KB”, “MB”, “GB”, “TB”, “PB”, “EB”, “ZB”, “YB” in short respectively.

Output
For each test case, output one line “Case #x: y”, where x is the case number (starting from 1) and y is the percentage of the “missing part”. The answer should be rounded to two digits after the decimal point.

Sample

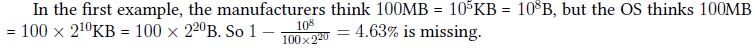
模拟题。

	int main(){
	int n;
	char u[8];
	while (scanf("%d", &n) != EOF) {
	for (int cas = 1; cas <= n; cas++) {
	scanf("%*d%s", u);
	printf("Case #%d: ", cas);
	if (u[1] == 'B')
	printf("0.00");
	else if (u[1] == 'K')
	printf("2.34");
	else if (u[1] == 'M')
	printf("4.63");
	else if (u[1] == 'G')
	printf("6.87");
	else if (u[1] == 'T')
	printf("9.05");
	else if (u[1] == 'P')
	printf("11.18");
	else if (u[1] == 'E')
	printf("13.26");
	else if (u[1] == 'Z')
	printf("15.30");
	else if (u[1] == 'Y')
	printf("17.28");
	printf("%%\n");
	}
	}
	return 0;
	}

# 头文件

# A - Chinese Zodiac

# B - Count Color

# C - Stealing Harry Potter's Precious

# D - Football

# E - Graph Game

# F - Hard Code

# G - Hard Disk Drive

Weekly Contest 1 - UM ICPC Training Group

Latex模板 适用于Assignment Report和Presentation

Latex模板适用于Assignment Report和Presentation